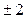题目内容
(本
 小题满分14分)已知
小题满分14分)已知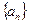 是正数组成的数列,
是正数组成的数列,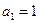 ,且点(
,且点(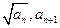 )(n
)(n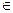 N*)在
N*)在 函数
函数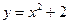 的图象上.(Ⅰ)求数列
的图象上.(Ⅰ)求数列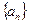 的通项公式;
的通项公式; (Ⅱ)若
(Ⅱ)若
 数列
数列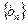
 满足
满足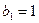 ,
,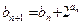 ,求数列
,求数列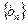 的通项公式.
的通项公式.

 小题满分14分)已知
小题满分14分)已知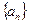 是正数组成的数列,
是正数组成的数列,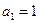 ,且点(
,且点(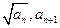 )(n
)(n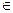 N*)在
N*)在 函数
函数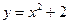 的图象上.(Ⅰ)求数列
的图象上.(Ⅰ)求数列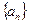 的通项公式;
的通项公式; (Ⅱ)若
(Ⅱ)若
 数列
数列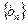
 满足
满足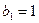 ,
,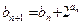 ,求数列
,求数列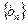 的通项公式.
的通项公式.(Ⅰ2n-1. (Ⅱ)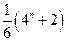
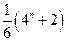
(Ⅰ)由已知得an+ 1=an
1=an +2,即an+1-an=2,又a1=1,所以数列{an}是以1为首项,公差为2的等差数列. 故an=1+(n-1)×
+2,即an+1-an=2,又a1=1,所以数列{an}是以1为首项,公差为2的等差数列. 故an=1+(n-1)× 2="2n-1. "
2="2n-1. "
( Ⅱ)由(Ⅰ)知:an=2n-1从而bn+1-bn=
Ⅱ)由(Ⅰ)知:an=2n-1从而bn+1-bn=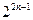 .
.
bn=(bn-bn- 1)+(bn-1-bn-2)+···+(
1)+(bn-1-bn-2)+···+( b2-b1)+b1
b2-b1)+b1
=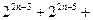 ···
···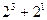 +1=
+1=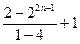 =
= .
.
 1=an
1=an +2,即an+1-an=2,又a1=1,所以数列{an}是以1为首项,公差为2的等差数列. 故an=1+(n-1)×
+2,即an+1-an=2,又a1=1,所以数列{an}是以1为首项,公差为2的等差数列. 故an=1+(n-1)× 2="2n-1. "
2="2n-1. " (
 Ⅱ)由(Ⅰ)知:an=2n-1从而bn+1-bn=
Ⅱ)由(Ⅰ)知:an=2n-1从而bn+1-bn=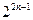 .
. bn=(bn-bn-
 1)+(bn-1-bn-2)+···+(
1)+(bn-1-bn-2)+···+( b2-b1)+b1
b2-b1)+b1 =
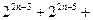 ···
···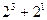 +1=
+1=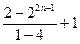 =
= .
. 
练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 中,
中,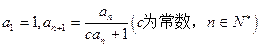 ,且
,且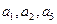 成公比不等于1的等比数列
成公比不等于1的等比数列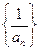 是等差数列; (2)求c的值;
是等差数列; (2)求c的值;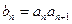 ,数列
,数列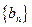 的前
的前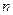 项和为
项和为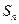 ,求
,求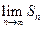
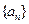 是公方差为
是公方差为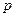 (p>0,an >0)的等方差数列,
(p>0,an >0)的等方差数列,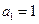 求
求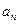 的通项公式;
的通项公式;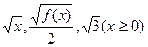 成等差数列.又数列
成等差数列.又数列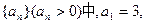 此数列的前n项的和Sn(
此数列的前n项的和Sn(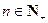 )对所有大于1的正整数n都有
)对所有大于1的正整数n都有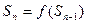 .(1)求数列
.(1)求数列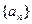 的第n+1项;(2)若
的第n+1项;(2)若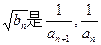 的等比中项,且Tn为{bn}的前n项和,求Tn.
的等比中项,且Tn为{bn}的前n项和,求Tn. 已知函数
已知函数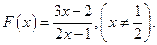
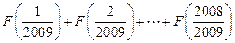 ;(2)已知数列
;(2)已知数列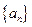 满足
满足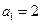 ,
,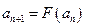 ,求数列
,求数列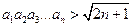 .
. ,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4 (Ⅰ)求证:数列{bn}中的每一项都是数列{an}中的项;
,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4 (Ⅰ)求证:数列{bn}中的每一项都是数列{an}中的项; ,求数列{cn}的前n项的和Tn
,求数列{cn}的前n项的和Tn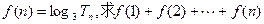 的最大值.
的最大值.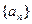 中,前n项和为
中,前n项和为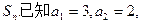
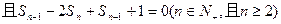
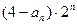 }的前n项和Tn.
}的前n项和Tn. 中,已知
中,已知 则
则 等于
等于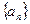 是递增等差数列,前三项的和为12,前三项的积为48,则它的公差为( )
是递增等差数列,前三项的和为12,前三项的积为48,则它的公差为( )