题目内容
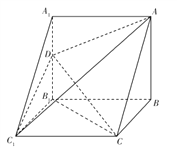
【题目】如图所示,直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 为棱
为棱![]() 的中点.
的中点.
(Ⅰ)探究直线![]() 与平面
与平面![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(Ⅱ)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)见解析(Ⅱ)![]() .
.
【解析】试题分析:(I)连接![]() ,设
,设![]() ,则
,则![]() 为
为![]() 的中点由三角形中位线定理可得四边形
的中点由三角形中位线定理可得四边形![]() 为平行四边形,由线面平行的判定定理可得
为平行四边形,由线面平行的判定定理可得![]() 平面
平面![]() ;(II)由点
;(II)由点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,再利用“等积变换”可得
的距离,再利用“等积变换”可得![]() ,进而可得三棱锥
,进而可得三棱锥![]() 的体积.
的体积.
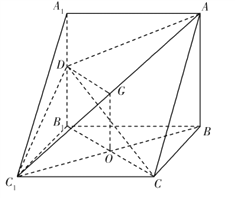
试题解析:(Ⅰ)连接![]() ,设
,设![]() ,因为四边形
,因为四边形![]() 为矩形,所以
为矩形,所以![]() 为
为![]() 的中点.
的中点.
设![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
, ![]() ,则
,则![]() ,且
,且![]() .
.
由已知![]() ,且
,且![]() ,则
,则![]() ,且
,且![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,即
,即![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)易知![]() 平面
平面![]() ,由(Ⅰ)可知,
,由(Ⅰ)可知, ![]() 平面
平面![]() .
.
所以点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,
的距离,
所以![]() .因为
.因为![]() ,
,
所以![]() ,
,
故三棱锥![]() 的体积为
的体积为![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
【题目】将参加数学竞赛的1000名学生编号如下:0001,0002,0003,…,1000,按系统抽样的方法从中抽取一个容量为50的样本,如果在第一组抽得的编号是0015,则在第21组抽得的编号是 .
【题目】某教师调查了![]() 名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
男生 | 女生 | 总计 | |
购买数学课外辅导书超过 |
|
|
|
购买数学课外辅导书不超过 |
|
|
|
总计 |
|
|
|
(Ⅰ)根据表格中的数据,是否有![]() 的把握认为购买数学课外辅导书的数量与性别相关;
的把握认为购买数学课外辅导书的数量与性别相关;
(Ⅱ)从购买数学课外辅导书不超过![]() 本的学生中,按照性别分层抽样抽取
本的学生中,按照性别分层抽样抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人询问购买原因,求恰有
人询问购买原因,求恰有![]() 名男生被抽到的概率.
名男生被抽到的概率.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|


