题目内容
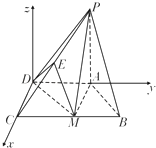
【题目】已知四棱锥P﹣ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形, ![]() .
. 
(1)求证:平面PAM⊥平面PDM;
(2)若点E为PC中点,求二面角P﹣MD﹣E的余弦值.
【答案】
(1)证明:∵△ABM是边长为2的等边三角形,底面ABCD是直角梯形,∴ ![]() ,
,
又 ![]() ,∴CM=3,∴AD=3+1=4,∴AD2=DM2+AM2,∴DM⊥AM.
,∴CM=3,∴AD=3+1=4,∴AD2=DM2+AM2,∴DM⊥AM.
又PA⊥底面ABCD,∴DM⊥PA,∴DM⊥平面PAM,
∵DM平面PDM,∴平面PAM⊥平面PDM.
(2)解:以D为原点,DC所在直线为x轴,DA所在直线为y轴,
过D且与PA平行的直线为z轴,建立空间直角坐标系D﹣xyz,
则 ![]() ,
, ![]() ,
, ![]() ,
,
设平面PMD的法向量为 ![]() ,
,
则 ![]() ,
,
取x1=3,∴ ![]() .
.
∵E为PC中点,则 ![]() ,CD
,CD
设平面MDE的法向量为 ![]() ,
,
则 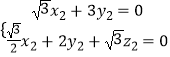 ,取x2=3,∴
,取x2=3,∴ ![]() .
.
由 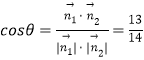 .
.
∴二面角P﹣MD﹣E的余弦值为 ![]()
【解析】(1)证明DM⊥AM.DM⊥PA,推出DM⊥平面PAM,即可证明平面PAM⊥平面PDM.(2)以D为原点,DC所在直线为x轴,DA所在直线为y轴,过D且与PA平行的直线为z轴,建立空间直角坐标系D﹣xyz,求出平面PMD的法向量,平面MDE的法向量,利用向量的 数量积求解二面角P﹣MD﹣E的余弦值.

练习册系列答案
相关题目