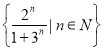题目内容
【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题：将1，2，3，4，5，6，7，8，9分别填入3×3的方格中，使得每一行，每一列及对角线上的三个数的和都相等(如图所示)，我们规定：只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同，就称为不同的幻方，那么不同的三阶幻方的个数是（ ）
4 | 9 | 2 |
3 | 5 | 7 |
8 | 1 | 6 |
A.9B.8C.6D.4
【答案】B
【解析】
首先如题设分析，每行每列的所有书的和都是15，然后列举所有3个数的和为15的组合情况，含5的有5个，所以5放中间，含2，4，6，8的都3个，所以放在四个角处，并且456，258分占两条对角线，再用列举法即可得到结论.
因为所有数的和为
，
，所以每行每列，以及对角线的和都是15，采用列举法：492、357、816；276、951、438；294、753、618；438、951、276；816、357、492；618、753、294；672、159、834；834、159、672.共8种排法，则不同的三阶幻方的个数是8.
故选：B.
练习册系列答案
相关题目
