题目内容
【题目】设集合
是实数集
的子集,如果正实数
满足:对任意
都存在
使得
则称为集合的一个“跨度”，已知三个命题:
(1)若为集合的“跨度”,则
也是集合的“跨度”；
(2)集合
的“跨度”的最大值是4；
(3)
是集合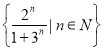
的“跨度”.
这三个命题中正确的个数是（）
A.0B.1C.2D.3
【答案】B
【解析】
根据集合新定义，对“跨度”的理解，对三个选项逐一验证即可
（1）若集合为
，则集合的“跨度”为1，不存在2是集合的“跨度”，故（1）错
（2）集合可表示为
，集合相当于是从
无限往两边扩充的数列，比如
时，若取
，我们会发现
的绝对值都是在不断变大，故
值会不断增大，故的值会无限扩大，集合中不存在 “跨度”最大值的说法
（3）集合可表示为
，当集合中的
时，
，因集合中含有元素
，我们令
，则
，故集合的 “跨度”可以为
正确的命题为（3）
故选：B
练习册系列答案
相关题目
