题目内容
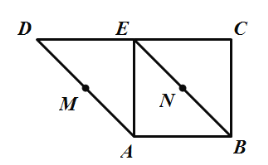
【题目】如图，某公园有三条观光大道
、
、
围成直角三角形，其中直角边
，斜边
.
（1）若甲乙都以每分钟100
的速度从点
出发，甲沿
运动，乙沿运动，乙比甲迟2分钟出发，求乙出发后的第1分钟末甲乙之间的距离；
（2）现有甲、乙、丙三位小朋友分别在点
、
、
，设
，乙丙之间的距离
是甲乙之间距离
的2倍，且
，请将甲乙之间的距离
表示为
的函数，并求甲乙之间的最小距离.
【答案】（1）
；（2）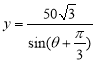
， 
.
【解析】
（1）先求出角
，在三角形BDE中，
，
，利用余弦定理求出
；（2）先在
中求出
，在
中由正弦定理得
代入得出
与
的关系，求出最小值.
（1）依题意得，，在
中
在中，由余弦定理得
.
（2）由题意得
，在
中，
，
在中由正弦定理得
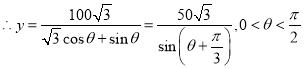
所以当
时，有最小值
. 即甲乙之间的最小距离为
.
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
