题目内容
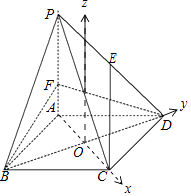
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为 3 的菱形,∠ABC=60°,PA⊥平面ABCD,PA=3,F 是棱 PA上的一个动点,E为PD的中点.
(Ⅰ)若 AF=1,求证:CE∥平面 BDF;
(Ⅱ)若 AF=2,求平面 BDF 与平面 PCD所成的锐二面角的余弦值.
【答案】证明:(Ⅰ)如图所示,取PF中点G,连接EG,CG. 连接AC交BD于O,连接FO.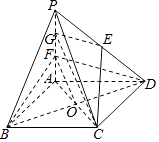
由题可得F为AG中点,O为AC中点,
∴FO∥GC;
又G为PF中点,E为PD中点,
∴GE∥FD.
又GE∩GC=G,GE、GC面GEC,
FO∩FD=F,FO,FD面FOD.
∴面GEC∥面FOD.
∵CE面GEC,
∴CE∥面BDF;
(Ⅱ)解:∵底面ABCD是边长为 3 的菱形,
∴AC⊥BD,设交点为O,以O为坐标原点建立如图所示空间直角坐标系,
则B(0,﹣ ![]() ,0),D(0,
,0),D(0, ![]() ,0),P(﹣
,0),P(﹣ ![]() ,0,3),C(
,0,3),C( ![]() ,0,0),F(-
,0,0),F(- ![]() ,0,2).
,0,2).
则 ![]() ,
, 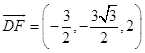 ,
, 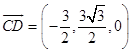 ,
,  .
.
设平面BDF的一个法向量为 ![]() ,
,
则 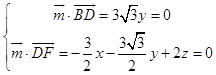 ,取z=3,得
,取z=3,得 ![]() .
.
设平面PCD的一个法向量为 ![]() ,
,
则 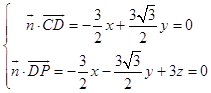 ,取y=
,取y= ![]() ,得
,得 ![]() .
.
∴cos< ![]() >=
>= ![]() =
= ![]() .
.
∴平面 BDF 与平面 PCD所成的锐二面角的余弦值为 ![]() .
.
【解析】(Ⅰ)取PF中点G,连接EG,CG.连接AC交BD于O,连接FO.由三角形中位线定理可得FO∥GC,GE∥FD.然后利用平面与平面平行的判定得到面GEC∥面FOD,进一步得到CE∥面BDF;(Ⅱ)由底面ABCD是边长为 3 的菱形,可得AC⊥BD,设交点为O,以O为坐标原点建立如图所示空间直角坐标系,求出所用点的坐标,再求出平面 BDF 与平面 PCD的一个法向量,由两法向量所成角的余弦值求得平面 BDF 与平面 PCD所成的锐二面角的余弦值.

 阅读快车系列答案
阅读快车系列答案【题目】为了解人们对于国家新颁布的“生育二孩放开”政策的热度,现在对某市年龄在35岁的人调查,随机选取年龄在35岁的100人进行调查,得到他们的情况为:在55名男性中,支持生二孩的有40人,不支持生二孩的有15人;在45名女性中,支持生二孩的有20人,不支持的有25人.
(Ⅰ)完成下面2×2列联表,并判断有多大的把握认为“支持生二孩与性别有关”?
支持生二孩 | 不支持生二孩 | 合计 | |
男性 | |||
女性 | |||
合计 |
附:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.150 | 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(Ⅱ)在被调查的人员中,按分层抽样的方法从支持生二孩的人中抽取6人,再用简单随机抽样的方法从这6人中随机抽取2人,求这2人中恰好有1名男性的概率;
(Ⅲ)以上述样本数据估计总体,从年龄在35岁人中随机抽取3人,记这3人中支持生二孩且为男性的人数为X,求X的分布列和数学期望.

