题目内容
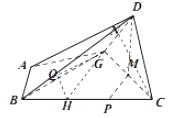
【题目】在四边形ABCD中(如图①),AB∥CD,AB⊥BC,G为AD上一点,且AB=AG=1,GD=CD=2,M为GC的中点,点P为边BC上的点,且满足BP=2PC.现沿GC折叠使平面GCD⊥平面ABCG(如图②). 
(1)求证:平面BGD⊥平面GCD:
(2)求直线PM与平面BGD所成角的正弦值.
【答案】
(1)证明:在直角梯形ABCD中,AB=AG=1,GD=CD=2,BC=2 ![]() ,cosD=
,cosD= ![]() ,
,
∴GC= ![]() =
= ![]() ,BG=
,BG= ![]() ,
,
∴BG2+GC2=BC2,∴BG⊥GC,
∵平面GCD⊥平面ABCG,平面GCD∩平面ABCG=GC,
∴BG⊥平面GCD,
∵BG平面GCD,
∴平面BGD⊥平面GCD
(2)解:取BP的中点H,连接GH,则GH∥MP,作HQ⊥平面BGD,连接GQ,则∠HGQ为直线GH与平面BGD所成的角,即直线PM与平面BGD所成角.
由(1),作CN⊥GD,则CN⊥平面BGD,
∵HQ⊥平面BGD,
∴HQ∥GN,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴HQ= ![]() CN.
CN.
△DGC中,GC= ![]() ,DM=
,DM= ![]() ,
,
由GDCN=GCDM,得CN= ![]() ,
,
∴HQ= ![]() ,
,
∵直角梯形ABCD中,GH= ![]() ,∴sin∠HGQ=
,∴sin∠HGQ= ![]() =
= ![]() ,
,
∴直线PM与平面BGD所成角的正弦值为 ![]() .
.
【解析】(1)利用勾股定理,证明BG⊥GC,根据平面与平面垂直的性质,证明BG⊥平面GCD,即可证明平面BGD⊥平面GCD:(2)取BP的中点H,连接GH,则GH∥MP,作HQ⊥平面BGD,连接GQ,则∠HGQ为直线GH与平面BGD所成的角,即直线PM与平面BGD所成角.
【考点精析】根据题目的已知条件,利用平面与平面垂直的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则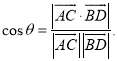 .
.

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案