题目内容
【题目】数列{an}是公比为q（q＞1）的等比数列，其前n项和为Sn ． 已知S3=7，且3a2是a1+3与a3+4的等差数列． （Ⅰ）求数列{an}的通项公式an；
（Ⅱ）设bn= 
，cn=bn（bn+1﹣bn+2），求数列{cn}的前n项和Tn ．
【答案】解：（Ⅰ）依题意，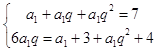 
，解得： 
， ∴数列{an}的通项公式an=2n﹣1；
（Ⅱ）∵bn= 
= 
，cn=bn（bn+1﹣bn+2）= （ 
﹣ 
）=（ ﹣ ）﹣ 
（ ﹣ ），
∴Tn=c1+c2+…+cn=[（1﹣ ）﹣ （ 
﹣ 
）]+[（ ﹣ ）﹣ （ ﹣ 
）]+…+[（ ﹣ ）﹣ （ ﹣ ）]
=（1﹣ ）﹣ （1﹣ + ﹣ + ﹣ 
+…+ ﹣ ）
= 
﹣ （1+ ﹣ ﹣ ）
= ﹣ 
．
【解析】（Ⅰ）依题意，可得， 
，解得首项与公比，即可求得等比数列{an}的通项公式an；（Ⅱ）由an=2n﹣1可得bn= 
= 
，cn=bn（bn+1﹣bn+2）=（ ﹣ 
）﹣ 
（ ﹣ 
），利用裂项法与分组求和法即可求得数列{cn}的前n项和Tn ．
【考点精析】认真审题，首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系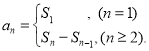
)，还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键．
【题目】某校高三共有900名学生，高三模拟考之后，为了了解学生学习情况，用分层抽样方法从中抽出若干学生此次数学成绩，按成绩分组，制成如下的频率分布表：
组号 | 第一组 | 第二组 | 第二组 | 第四组 |
分组 | [70，80） | [80，90） | [90，100） | [100，110） |
频数 | 6 | 4 | 22 | 20 |
频率 | 0.06 | 0.04 | 0.22 | 0.20 |
组号 | 第五组 | 第六组 | 第七组 | 第八组 |
分组 | [110，120） | [120，130） | [130，140） | [140，150] |
频数 | 18 | a | 10 | 5 |
频率 | b | 0.15 | 0.10 | 0.05 |
（1）若频数的总和为c，试求a，b，c的值；
（2）为了了解数学成绩在120分以上的学生的心理状态，现决定在第六、七、八组中用分层抽样方法抽取6名学生，在这6名学生中又再随机抽取2名与心理老师面谈，令第七组被抽中的学生数为随机变量ξ，求随机变量ξ的分布列和数学期望；
（3）估计该校本次考试的数学平均分．