题目内容
【题目】已知函数f（x）=|x﹣m|（m＞0），g（x）=2f（x）﹣f（x+m），g（x）的最小值为﹣1． （Ⅰ）求m的值；
（Ⅱ）若|a|＜m，|b|＜m，且a≠0．求证：f（ab）＞|a|f（ 
）．
【答案】解：（Ⅰ）∵f（x）=|x﹣m|（m＞0）， ∴g（x）=2f（x）﹣f（x+m）=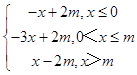 
，
故当x=m时，函数取最小值﹣m=﹣1，
解得：m=1；
（Ⅱ）证明：要证f（ab）＞|a|f（ 
）．
即证|ab﹣1|＞|a﹣b|，
∵|a|＜1，|b|＜1，
∴（ab﹣1）2﹣（a﹣b）2=（a2b2﹣2ab+1）﹣（a2﹣2ab+b2）=（a2﹣1）（b2﹣1）＞0，
即（ab﹣1）2＞（a﹣b）2 ，
∴|ab﹣1|＞|a﹣b|，
∴f（ab）＞|a|f（ ）
【解析】（Ⅰ）根据函数f（x）=|x﹣m|（m＞0），可得函数g（x）的解析式，进而构造方程，可得m的值；（Ⅱ）若|a|＜m，|b|＜m，要证f（ab）＞|a|f（ 
）．即证|ab﹣1|＞|a﹣b|平方可得结论．
练习册系列答案
相关题目
