题目内容

12．四名同学报名参加三项课外活动，每人限报其中一项，不同报名方法共有（　　）
A．12B．64C．81D．7

分析 根据题意，易得四名同学中每人有3种报名方法，由分步计数原理计算可得答案．

解答 解：四名同学报名参加三项课外活动，每人限报其中一项，
每人有3种报名方法；
根据分计数原理，可得共有3×3×3×3=81种不同的报名方法；
故选：C．

点评 本题考查分步计数原理的运用，解题时注意题干条件中“每人限报一项”．

练习册系列答案
相关题目
2．已知函数f（x）=Asin（x+φ）（A＞0，0＜φ＜π），x∈R的最大值是1，其图象经过点M（$\frac{π}{3}$，$\frac{1}{2}$）．
（1）求函数f（x）的解析式；
（2）已知f（$\frac{π}{4}$-α）=-$\frac{4}{5}$，且α∈（-$\frac{3π}{4}$，-$\frac{π}{4}$），求$\frac{1+sin2α+cos2α}{1+tanα}$的值．
3．已知△ABC的三个内角A，B，C所对的边分别为a、b、c，向量$\overrightarrow{m}$=（2sin$\frac{A}{2}$，$\sqrt{3}$），$\overrightarrow{n}$=（cosA，2cos2$\frac{A}{4}$-1），且$\overrightarrow{m}$∥$\overrightarrow{n}$．
（1）求角A的大小；
（2）若|$\overrightarrow{a}$|=$\sqrt{7}$且△ABC的面积为$\frac{3\sqrt{3}}{2}$，求b，c的值．
20．若函数f（x）=sinx+ax在R上单调递增，则实数a的取值范围为（　　）
A．[-1，1]B．（-∞，-1]C．（-∞，1]D．[1，+∞）
7．某校有6间不同的电脑室，每天晚上至少开放2间，求不同安排方案的种数，现有四位同学分别给出下列四个结果①$C_6^2$；②26-7；③$C_6^3+2C_6^4+C_6^5+C_6^6$，其中正确的结论是（　　）
A．①B．②与③C．①与②D．①②③
17．若下表数据对应的y关于x的线性回归方程为$\hat y=0.7x+a$，则a=0.35．
x3456
y2.5344.5
4．从2010名学生中选50人组成参观团，先用简单随机抽样方法剔除10人，再将其余2000人从0到1999编号，按等距系统抽样方法选取，若第一组采用抽签法抽到的号码是30，则最后一组入选的号码是（　　）
A．1990B．1991C．1989D．1988
1．函数f（x）=lnx-$\frac{1}{2}{x^2}$的单调递增区间为（　　）
A．（-∞，-1）与（1，+∞）B．（0，1）∪（1，+∞）C．（0，1）D．（1，+∞）
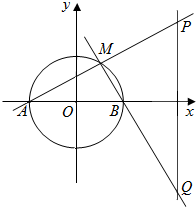2．在平面直角坐标系xOy中，圆O：x2+y2=4交x轴于点A，B（点A在x轴的负半轴上），点M为圆O上一动点，MA，MB分别交直线x=4于P，Q两点．
（1）求P，Q两点纵坐标的乘积；
（2）若点C的坐标为（1，0），连接MC交圆O于另一点N：
①试判断点C与以PQ为直径的圆的位置关系，并说明理由；
②记MA，NA的斜率分别为k1，k2，试探究k1k2是否为定值？若是，请求出该定值；若不是，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网