题目内容
2.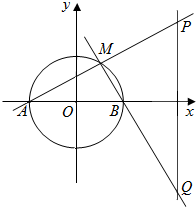 在平面直角坐标系xOy中,圆O:x2+y2=4交x轴于点A,B(点A在x轴的负半轴上),点M为圆O上一动点,MA,MB分别交直线x=4于P,Q两点.
在平面直角坐标系xOy中,圆O:x2+y2=4交x轴于点A,B(点A在x轴的负半轴上),点M为圆O上一动点,MA,MB分别交直线x=4于P,Q两点.(1)求P,Q两点纵坐标的乘积;
(2)若点C的坐标为(1,0),连接MC交圆O于另一点N:
①试判断点C与以PQ为直径的圆的位置关系,并说明理由;
②记MA,NA的斜率分别为k1,k2,试探究k1k2是否为定值?若是,请求出该定值;若不是,请说明理由.
分析 (1)求出直线AM的方程,求出$P(4,\frac{{6{y_0}}}{{{x_0}+2}})$,$Q(4,\frac{{2{y_0}}}{{{x_0}-2}})$,然后求解P,Q两点纵坐标的乘积;
(2)通过$\overrightarrow{CP}•\overrightarrow{CQ}=9+\frac{{6{y_0}}}{{{x_0}+2}}•\frac{{2{y_0}}}{{{x_0}-2}}=-3$,判断点C在圆内,设M(x1,y1),N(x2,y2),当直线MN的斜率不存在时,$M(1,\sqrt{3})$,$N(1,-\sqrt{3})$,求出直线的斜率,当直线MN的斜率存在时,设直线MN的方程为y=k(x-1),代入圆方程x2+y2=4,利用韦达定理化简求解k1k2的值.
解答 解:(1)由题意,解得A(-2,0),B(2,0),设M(x0,y0),∴直线AM的方程为$y=\frac{y_0}{{{x_0}+2}}(x+2)$,令x=4,则$y=\frac{{6{y_0}}}{{{x_0}+2}}$,∴$P(4,\frac{{6{y_0}}}{{{x_0}+2}})$,同理$Q(4,\frac{{2{y_0}}}{{{x_0}-2}})$,∴${y_P}{y_Q}=\frac{{6{y_0}}}{{{x_0}+2}}•\frac{{2{y_0}}}{{{x_0}-2}}=\frac{{12{y_0}^2}}{{{x_0}^2-4}}=-12$…(5分)
(2)①∵C(1,0),由(1)知$\overrightarrow{CP}=(3,\frac{{6{y_0}}}{{{x_0}+2}})$,$\overrightarrow{CQ}=(3,\frac{{2{y_0}}}{{{x_0}-2}})$,
∴$\overrightarrow{CP}•\overrightarrow{CQ}=9+\frac{{6{y_0}}}{{{x_0}+2}}•\frac{{2{y_0}}}{{{x_0}-2}}=-3$,即$∠PCQ>\frac{π}{2}$,
∴点C在圆内…(10分)
②设M(x1,y1),N(x2,y2),当直线MN的斜率不存在时,$M(1,\sqrt{3})$,$N(1,-\sqrt{3})$,此时${k_1}{k_2}=-\frac{1}{3}$;
当直线MN的斜率存在时,设直线MN的方程为y=k(x-1),
代入圆方程x2+y2=4,整理得(1+k2)x2-2k2x+k2-4=0,
∴${x_1}+{x_2}=\frac{{2{k^2}}}{{1+{k^2}}}$,${x_1}{x_2}=\frac{{{k^2}-4}}{{1+{k^2}}}$,又${k_1}{k_2}=\frac{{{y_1}{y_2}}}{{({x_1}+2)({x_2}+2)}}=\frac{{{k^2}({x_1}{x_2}-{x_1}-{x_2}+1)}}{{{x_1}{x_2}+2({x_1}+{x_2})+4}}$,
∴${k_1}{k_2}={k^2}\frac{{\frac{{{k^2}-4}}{{1+{k^2}}}-\frac{{2{k^2}}}{{1+{k^2}}}+1}}{{\frac{{{k^2}-4}}{{1+{k^2}}}+\frac{{4{k^2}}}{{1+{k^2}}}+4}}=-\frac{1}{3}$…(16分)
点评 本题考查直线与圆的方程的综合应用,直线与圆的位置关系,考查计算能力.

| A. | 12 | B. | 64 | C. | 81 | D. | 7 |
| A. | 12 | B. | 6 | C. | 4$\sqrt{5}$ | D. | 2$\sqrt{5}$ |