题目内容
10.已知函数f(x)=$\frac{lnx}{x}$,且对于?x∈R(x≠0),都有g(x)•f(ex)=1.(1)求g(x)的解析式.并写出函数g(x)的单调区间;
(2)已知正数a,b,c:clnb=a+clnc且c≤2a,求$\frac{b}{a}$的最小值.
(3)在 区间[1,+∞)是否存在相异实数x1,x2,使得f(g(x1))=f(g(x2)),若存在,给出一组数值,若不存在,请说明理由.
分析 (1)先求出f(ex),代入g(x)•f(ex)=1,从而求出g(x)的表达式;
(2)由clnb=a+clnc化为lnb=$\frac{a}{c}$+lnc,可得ln$\frac{b}{a}$=lnb-lna=$\frac{a}{c}$+ln$\frac{c}{a}$,令$\frac{c}{a}$=x,可得ln$\frac{b}{a}$=f(x)=$\frac{1}{x}$+lnx,0<x<2.再利用导数研究其单调性极值与最值即可;
(3)问题转化为存在f(x1)=f(x2),求出函数f(x)的导数,得到函数的单调区间,求出函数的值域,画出函数的图象,通过图象读出即可.
解答 解:(1)∵函数f(x)=$\frac{lnx}{x}$,
∴f(ex)=$\frac{l{ne}^{x}}{{e}^{x}}$=$\frac{x}{{e}^{x}}$,
由g(x)•f(ex)=1,
得:g(x)=$\frac{1}{f{(e}^{x})}$=$\frac{{e}^{x}}{x}$,
∴g′(x)=$\frac{{e}^{x}(x-1)}{{x}^{2}}$,
令g′(x)>0,解得:x>1,令g′(x)<0,解得:x<1且x≠0,
∴g(x)在(-∞,0),(0,1)递减,在(1,+∞)递增;
(2)由clnb=a+clnc化为lnb=$\frac{a}{c}$+lnc,
∴ln$\frac{b}{a}$=lnb-lna=$\frac{a}{c}$+lnc-lna=$\frac{a}{c}$+ln$\frac{c}{a}$,
令x=$\frac{c}{a}$,由a,b,c为正数且c<2a,
得:0<$\frac{c}{a}$<2,∴0<x<2,
则ln$\frac{b}{a}$=h(x)=$\frac{1}{x}$+lnx,(0<x<2),
h′(x)=-$\frac{1}{{x}^{2}}$+$\frac{1}{x}$=$\frac{x-1}{{x}^{2}}$,
令h′(x)>0,解得:x>1,令h′(x)<0,解得:x<1,
∴h(x)在(0,1)递减,在(1,2)递增,
∴h(x)最小值=h(1)=1,
∴ln$\frac{b}{a}$的最小值是1,∴$\frac{b}{a}$的最小值是e;
(3)∵f(g(x1))=$\frac{ln\frac{{e}^{{x}_{1}}}{{x}_{1}}}{{x}_{1}}$=$\frac{l{ne}^{{x}_{1}}-l{nx}_{1}}{{x}_{1}}$=1-$\frac{l{nx}_{1}}{{x}_{1}}$,
f(g(x2))=$\frac{ln\frac{{e}^{{x}_{2}}}{{x}_{2}}}{{x}_{2}}$=$\frac{l{ne}^{{x}_{2}}-l{nx}_{2}}{{x}_{2}}$=1-$\frac{l{nx}_{2}}{{x}_{2}}$,
若存在f(g(x1))=f(g(x2)),即f(x1)=f(x2),
由f′(x)=$\frac{1-lnx}{{x}^{2}}$,令f′(x)>0,解得:0<x<e,令f′(x)<0,解得:x>e,
∴f(x)在[1,e)递增,在(e,+∞)递减,
∴f(x)最大值=f(x)极大值=f(e)=$\frac{1}{e}$,
而f(1)=0,x→+∞时,f(x)→0,
画出函数f(x)的图象,如图示: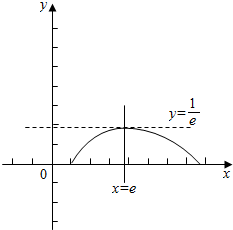 ,
,
不妨设x1<x2,
由图象得:在区间[1,e)上存在x1在(e,+∞)上存在x2,
使得f(g(x1))=f(g(x2)).
点评 本题考查函数的单调性、最值问题,考查导数的应用,考查了经过变形把问题转化为利用导数研究其单调性极值与最值,考查了推理能力和解决问题的能力.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案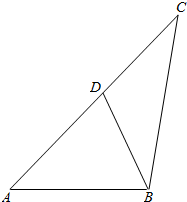 如图,在△ABC中,AB=2,AC=4,线段CB的垂直平分线交线段AC于D,AD-DB=1,则△BCD的面积为( )
如图,在△ABC中,AB=2,AC=4,线段CB的垂直平分线交线段AC于D,AD-DB=1,则△BCD的面积为( )| A. | $\frac{7}{10}$ | B. | $\frac{9}{10}$ | C. | 2 | D. | 8 |
| A. | [1,3] | B. | [$\sqrt{5}$-1,$\sqrt{5}$十1] | C. | [3-2$\sqrt{2}$,3+2$\sqrt{2}$] | D. | [4-2$\sqrt{3}$,4+2$\sqrt{3}$]. |
 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴长为2,过点A(4,1)的直线交椭圆于两个不同点M,N,若直线上另一点B满足|$\overrightarrow{AM}$|•|$\overrightarrow{BN}$|=|$\overrightarrow{AN}$|•|$\overrightarrow{BM}$|.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴长为2,过点A(4,1)的直线交椭圆于两个不同点M,N,若直线上另一点B满足|$\overrightarrow{AM}$|•|$\overrightarrow{BN}$|=|$\overrightarrow{AN}$|•|$\overrightarrow{BM}$|.