题目内容
3. 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴长为2,过点A(4,1)的直线交椭圆于两个不同点M,N,若直线上另一点B满足|$\overrightarrow{AM}$|•|$\overrightarrow{BN}$|=|$\overrightarrow{AN}$|•|$\overrightarrow{BM}$|.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴长为2,过点A(4,1)的直线交椭圆于两个不同点M,N,若直线上另一点B满足|$\overrightarrow{AM}$|•|$\overrightarrow{BN}$|=|$\overrightarrow{AN}$|•|$\overrightarrow{BM}$|.(Ⅰ)求点B的轨迹方程;
(Ⅱ)若点B的轨迹交椭圆于两个不同点P、Q,求△APQ的面积.
分析 (Ⅰ)运用椭圆的离心率公式和a,b,c的关系,可得椭圆方程,设过点A(4,1)的直线为y-1=k(x-4),
代入椭圆方程,运用韦达定理,由|$\overrightarrow{AM}$|•|$\overrightarrow{BN}$|=|$\overrightarrow{AN}$|•|$\overrightarrow{BM}$|可得$\frac{AM}{AN}$=$\frac{MB}{BN}$=$\frac{{x}_{1}-4}{{x}_{2}-4}$,设B(x,y),由向量的坐标表示,可得x,y关于k的式子,消去k,即可得到所求轨迹方程;
(Ⅱ)联立B的轨迹方程和椭圆方程,求得交点,再由三角形的面积公式,计算即可得到所求值.
解答 解:(Ⅰ)由题意可得e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,b=1,a2-1=c2,
解得a=2,c=$\sqrt{3}$,
即椭圆方程为$\frac{{x}^{2}}{4}$+y2=1,
设过点A(4,1)的直线为y-1=k(x-4),
代入椭圆方程可得(1+4k2)x2+8(1-4k)kx+64k2-32k=0,
设M(x1,y1),N(x2,y2),
判别式为64(1-4k)2k2-4(1+4k2)(64k2-32k)>0,
解得0<k<$\frac{3}{2}$,
则x1+x2=$\frac{8k(4k-1)}{1+4{k}^{2}}$,x1x2=$\frac{64{k}^{2}-32k}{1+4{k}^{2}}$,
由|$\overrightarrow{AM}$|•|$\overrightarrow{BN}$|=|$\overrightarrow{AN}$|•|$\overrightarrow{BM}$|可得
$\frac{AM}{AN}$=$\frac{MB}{BN}$=$\frac{{x}_{1}-4}{{x}_{2}-4}$,
设B(x,y),即有x=$\frac{{x}_{1}+\frac{{x}_{1}-4}{{x}_{2}-4}•{x}_{2}}{1+\frac{{x}_{1}-4}{{x}_{2}-4}}$=$\frac{2{x}_{1}{x}_{2}-4({x}_{1}+{x}_{2})}{{x}_{1}+{x}_{2}-8}$
=$\frac{4k}{k+1}$,
y=1+k(x-4)=1-k•$\frac{4}{k+1}$=$\frac{1-3k}{1+k}$,
消去k,可得x+y=1,(0<x<$\frac{12}{5}$),
则点B的轨迹方程为x+y=1,(0<x<$\frac{12}{5}$);
(Ⅱ)将x+y=1,(0<x<$\frac{12}{5}$)代入椭圆方程$\frac{{x}^{2}}{4}$+y2=1,
可得5x2-8x=0,解得x=0,或x=$\frac{8}{5}$,
即有交点为P(0,1),Q($\frac{8}{5}$,-$\frac{3}{5}$),
由AP∥x轴,可得Q到AP的距离为d=1+$\frac{3}{5}$=$\frac{8}{5}$,
则△APQ的面积为S=$\frac{1}{2}$|AP|d=$\frac{1}{2}$×4×$\frac{8}{5}$=$\frac{16}{5}$.
点评 本题考查椭圆的方程和性质,主要是离心率的运用,同时考查直线方程和椭圆方程联立,消去未知数,运用韦达定理,以及向量共线的坐标表示,考查运算能力,数轴画的图.

 口算题天天练系列答案
口算题天天练系列答案| A. | ($\frac{1}{2}$,1) | B. | ($\frac{1}{2}$,2) | C. | (1,$\frac{3}{2}$) | D. | (1,2) |
| A. | (-1,1) | B. | [-1,1] | C. | [-2,2] | D. | [0,2] |
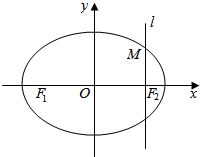 如图,在直角坐标系xOy中,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1和F2.过右焦点为F2且与x轴垂直的直线l与椭圆C相交,其中一个交点为M(1,$\frac{3}{2}$).(1)求椭圆C的方程:
如图,在直角坐标系xOy中,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1和F2.过右焦点为F2且与x轴垂直的直线l与椭圆C相交,其中一个交点为M(1,$\frac{3}{2}$).(1)求椭圆C的方程: