题目内容
2.已知函数f(x)=-$\frac{1}{6}$x3+x2-aex+2.(1)若a=1,求曲线y=f(x)在x=0处的切线方程;
(2)设函数y=f(x)在(a,b)上的导函数为f′(x),f′(x)在(a,b)上的导函数为f″(x).若在(a,b)上,f″(x)>0,则称函数在上为“凹函数”.若函数f(x)=-$\frac{1}{6}$x3+x2-aex+2是R上的“凹函数”,求实数a的取值范围.
分析 (1)求出函数的导数,求得切线的斜率和切点,由斜截式方程,即可得到切线方程;
(2)求出f(x)的导数,再求导数,由题意可得二阶导数大于0恒成立,由参数分离和构造函数求得最小值,即可得到a的范围.
解答 解:(1)函数f(x)=-$\frac{1}{6}$x3+x2-ex+2的导数为
f′(x)=-$\frac{1}{2}$x2+2x-ex,
即有曲线y=f(x)在x=0处的切线斜率为k=-1,
切点为(0,1),
则曲线y=f(x)在x=0处的切线方程为y=-x+1;
(2)函数f(x)=-$\frac{1}{6}$x3+x2-aex+2的导数为
f′(x)=-$\frac{1}{2}$x2+2x-aex,
f″(x)=-x+2-aex.
由函数f(x)=-$\frac{1}{6}$x3+x2-aex+2是R上的“凹函数”,
可得f″(x)>0恒成立,
即有a<$\frac{2-x}{{e}^{x}}$的最小值,
由函数y=$\frac{2-x}{{e}^{x}}$的导数为y′=$\frac{x-3}{{e}^{x}}$,
当x>3时,函数的导数大于0,函数递增;
当x<3时,喊话说的导数小于0,函数递减.
即有x=3处,函数y取得最小值,且为-e-3.
则a<-e-3.
点评 本题考查导数的运用:求切线方程和单调区间、极值和最值,考查新定义的理解和运用,同时考查不等式恒成立问题的解法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 某加油站工作人员根据以往该加油站的销售情况,绘制了该加油站日销售量的频率分布直方图,如图所示:
某加油站工作人员根据以往该加油站的销售情况,绘制了该加油站日销售量的频率分布直方图,如图所示: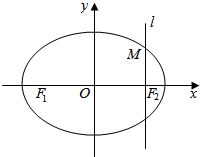 如图,在直角坐标系xOy中,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1和F2.过右焦点为F2且与x轴垂直的直线l与椭圆C相交,其中一个交点为M(1,$\frac{3}{2}$).(1)求椭圆C的方程:
如图,在直角坐标系xOy中,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1和F2.过右焦点为F2且与x轴垂直的直线l与椭圆C相交,其中一个交点为M(1,$\frac{3}{2}$).(1)求椭圆C的方程: