题目内容
点P是曲线 上的任意一点,则点P到直线y=x-2的最小距离为( )
上的任意一点,则点P到直线y=x-2的最小距离为( )
 上的任意一点,则点P到直线y=x-2的最小距离为( )
上的任意一点,则点P到直线y=x-2的最小距离为( )| A.1 | B. | C. | D. |
D
试题分析:曲线
 是
是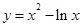 的图象,对函数求导
的图象,对函数求导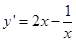 ,令
,令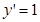 ,那么
,那么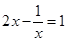 ,解得
,解得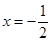 (舍去),
(舍去),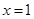 ,当
,当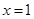 时,
时,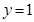 ,切点为
,切点为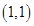 ,可得与直线y=x-2平行的切线方程为
,可得与直线y=x-2平行的切线方程为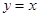 ,两平行线间距离,即为所求最小距离,由两平行线间的距离公式可得
,两平行线间距离,即为所求最小距离,由两平行线间的距离公式可得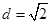 .
.
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
题目内容
 上的任意一点,则点P到直线y=x-2的最小距离为( )
上的任意一点,则点P到直线y=x-2的最小距离为( )| A.1 | B. | C. | D. |
 是
是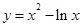 的图象,对函数求导
的图象,对函数求导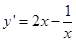 ,令
,令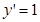 ,那么
,那么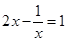 ,解得
,解得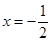 (舍去),
(舍去),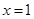 ,当
,当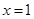 时,
时,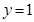 ,切点为
,切点为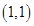 ,可得与直线y=x-2平行的切线方程为
,可得与直线y=x-2平行的切线方程为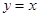 ,两平行线间距离,即为所求最小距离,由两平行线间的距离公式可得
,两平行线间距离,即为所求最小距离,由两平行线间的距离公式可得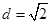 .
.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案