题目内容
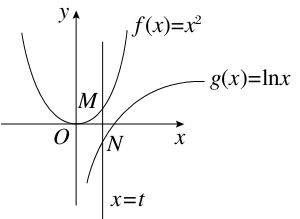
设直线x＝t与函数f(x)＝x2，g(x)＝lnx的图象分别交于点M，N，则当|MN|达到最小时t的值为________．
如图：|MN|＝f(t)－g(t)＝t2－lnt(t>0)，
令h(t)＝t2－lnt(t>0)，
则h′(t)＝2t－
＝
，
令h′(t)>0，得t>，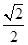
令h′(t)<0，得0<t<，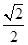
∴h(t)在(0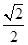，)上单调递减，在(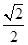，＋∞)上单调递增．
∴当t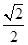＝时，h(t)取最小值，即t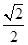＝时，|MN|取最小值．
令h(t)＝t2－lnt(t>0)，
则h′(t)＝2t－
＝，令h′(t)>0，得t>
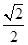，令h′(t)<0，得0<t<
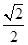，∴h(t)在(0，
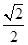)上单调递减，在(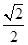，＋∞)上单调递增．∴当t＝
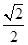时，h(t)取最小值，即t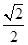＝时，|MN|取最小值．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
（
R），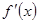
为其导函数，且
时
有极小值
．
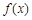的单调递减区间；
，
，当
时，对于任意x，
和
的值至少有一个是正数，求实数m的取值范围；
（
为正整数）对任意正实数
恒成立，求
，它们的定义域都是(0，e]，其中e是自然对数的底e≈2.7，a∈R.
对一切m，n∈(0，e]恒成立；
；
．
时，求
最小值；
是单调减函数，求
取值范围．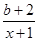
(x＞1)，其中b为实数．
上的任意一点，则点P到直线y=x-2的最小距离为( )
,则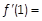
（ ）．
