题目内容
设函数 在R上存在导数
在R上存在导数 ,对任意的
,对任意的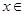 R,有
R,有 ,且
,且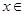 (0,+
(0,+ )时,
)时, .若
.若 ,则实数a的取值范围为( )
,则实数a的取值范围为( )
 在R上存在导数
在R上存在导数 ,对任意的
,对任意的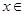 R,有
R,有 ,且
,且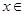 (0,+
(0,+ )时,
)时, .若
.若 ,则实数a的取值范围为( )
,则实数a的取值范围为( )| A.[1,+∞) | B.(-∞,1] | C.(-∞,2] | D.[2,+∞) |
B
试题分析:设
 ,
, ,
, ,所以
,所以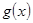 既是增函数又是奇函数,
既是增函数又是奇函数, ,由已知
,由已知 ,得
,得
 ,故选B.
,故选B.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R.
,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R. 对一切m,n∈(0,e]恒成立;
对一切m,n∈(0,e]恒成立; ,
, .
. 的极大值为
的极大值为 ,求实数
,求实数 的值;
的值; ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,若
,若 关于实数a 可线性分解,求
关于实数a 可线性分解,求 取值范围.
取值范围. ;
; .
. 上的任意一点,则点P到直线y=x-2的最小距离为( )
上的任意一点,则点P到直线y=x-2的最小距离为( )


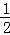 对称,且f′(1)=0
对称,且f′(1)=0 (
( )的图象如图所示,则不等式
)的图象如图所示,则不等式 的解集为________.
的解集为________.