题目内容
设函数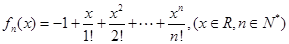
(Ⅰ)证明对每一个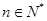 ,存在唯一的
,存在唯一的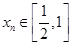 ,满足
,满足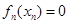 ;
;
(Ⅱ)由(Ⅰ)中的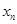 构成数列
构成数列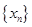 ,判断数列
,判断数列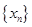 的单调性并证明;
的单调性并证明;
(Ⅲ)对任意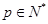 ,
,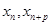 满足(Ⅰ),试比较
满足(Ⅰ),试比较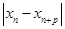 与
与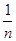 的大小.
的大小.
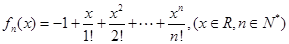
(Ⅰ)证明对每一个
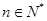 ,存在唯一的
,存在唯一的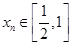 ,满足
,满足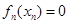 ;
;(Ⅱ)由(Ⅰ)中的
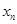 构成数列
构成数列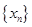 ,判断数列
,判断数列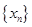 的单调性并证明;
的单调性并证明;(Ⅲ)对任意
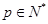 ,
,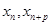 满足(Ⅰ),试比较
满足(Ⅰ),试比较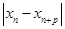 与
与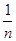 的大小.
的大小.(Ⅰ)详见解析;(Ⅱ)数列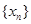 单调递减,证明详见解析;(Ⅲ)
单调递减,证明详见解析;(Ⅲ)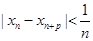 .
.
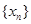 单调递减,证明详见解析;(Ⅲ)
单调递减,证明详见解析;(Ⅲ)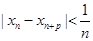 .
.试题分析:(Ⅰ)证明对每一个
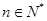 ,存在唯一的
,存在唯一的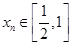 ,满足
,满足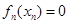 ,只需证明两点,第一证
,只需证明两点,第一证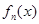 在
在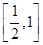 上为单调函数,第二证,
上为单调函数,第二证,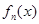 在区间
在区间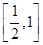 的端点的函数值异号,本题是高次函数,可用导数法判断单调性,而判断
的端点的函数值异号,本题是高次函数,可用导数法判断单调性,而判断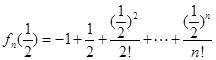 的符号是,可用放缩法;(Ⅱ)由(Ⅰ)中的
的符号是,可用放缩法;(Ⅱ)由(Ⅰ)中的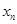 构成数列
构成数列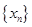 ,判断数列
,判断数列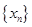 的单调性,由(Ⅰ)知
的单调性,由(Ⅰ)知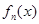 在
在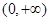 上递增,只需比较
上递增,只需比较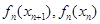 的大小,由(Ⅰ)知
的大小,由(Ⅰ)知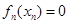 ,故
,故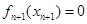 ,而
,而 ,从而得到
,从而得到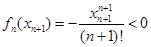 ,而
,而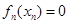 ,所以
,所以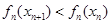 ,这样就可判断数列
,这样就可判断数列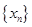 的单调性;(Ⅲ)对任意
的单调性;(Ⅲ)对任意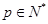 ,
,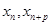 满足(Ⅰ),试比较
满足(Ⅰ),试比较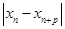 与
与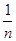 的大小,由(Ⅱ)知数列
的大小,由(Ⅱ)知数列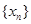 单调递减,故
单调递减,故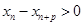 ,即比较
,即比较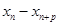 与
与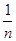 的大小,由(Ⅰ)知
的大小,由(Ⅰ)知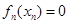 ,写出
,写出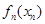 与
与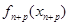 的式子,两式作差即可.本题函数与数列结合出题,体现学科知识交汇点的灵活运用,的确是一个好题,起到把关题的作用.
的式子,两式作差即可.本题函数与数列结合出题,体现学科知识交汇点的灵活运用,的确是一个好题,起到把关题的作用.试题解析:(Ⅰ)
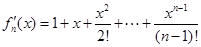 ,显然,当
,显然,当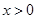 时,
时,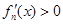 ,故
,故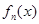 在
在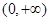 上递增,又
上递增,又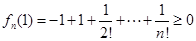 ,
,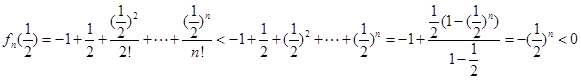 ,故存在唯一的
,故存在唯一的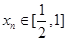 ,满足
,满足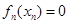 ;
;(Ⅱ)因为
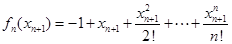 ,所以
,所以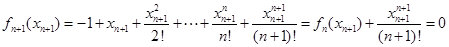 ,
,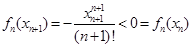 ,由(Ⅰ)知
,由(Ⅰ)知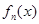 在
在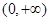 上递增,故
上递增,故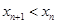 ,即数列
,即数列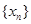 单调递减;
单调递减;(Ⅲ) 由(Ⅱ)数列
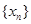 单调递减,故
单调递减,故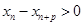 ,而
,而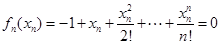 ,
,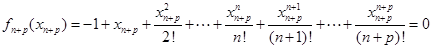 ,两式相减:并结合
,两式相减:并结合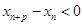 ,以及
,以及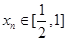 ,
,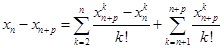
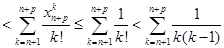
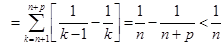 ,所以有
,所以有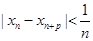 .
.
练习册系列答案
相关题目
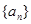 满足:
满足: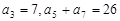 ,
,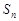 .
.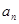 及
及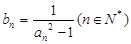 ,求数列
,求数列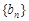 的前n项和
的前n项和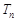 .
.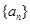 的前
的前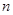 项和是
项和是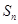 且
且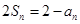
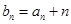 ,求数列
,求数列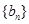 的前
的前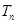 .
.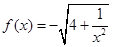 ,点
,点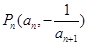 在曲线
在曲线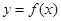 上
上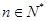 ,
,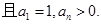 (Ⅰ)(Ⅰ)求数列
(Ⅰ)(Ⅰ)求数列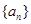 的通项公式;
的通项公式;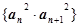 的前n项和为
的前n项和为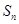 ,若对于任意的
,若对于任意的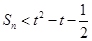 恒成立,求最小正整数t的值.
恒成立,求最小正整数t的值.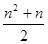
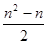
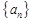 的前
的前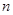 项和为
项和为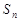 (
(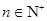 ), 关于数列
), 关于数列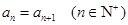 ,则
,则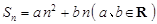 ,则
,则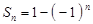 ,则
,则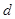 的等差数列
的等差数列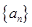 的前
的前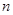 项和为
项和为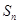 ,若
,若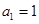 ,
, ,则当
,则当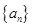
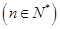 中,已知
中,已知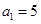 ,且在前
,且在前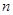 项和
项和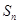 中,仅当
中,仅当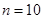 时,
时,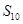 最大,则公差d满足( )
最大,则公差d满足( )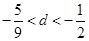
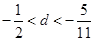
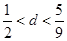
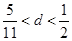
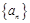 中,
中,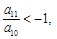 若它的前n项和
若它的前n项和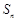 有最大值,则使
有最大值,则使 .
.