题目内容
某家电专卖店在五一期间设计一项有奖促销活动,每购买一台电视,即可通过电脑产生一组3个数的随机数组,根据下表兑奖:
| 奖次 | 一等奖 | 二等奖 | 三等奖 |
| 随机数组的特征 | 3个1或3个0 | 只有2个1或2个0 | 只有1个1或1个0 |
| 资金(单位:元) | 5m | 2m | m |
商家为了了解计划的可行性,估计奖金数,进行了随机模拟试验,并产生了20个随机数组,试验结果如下:
247,235,145,124,754,353,296,065,379,118,520,378,218,953,254,368,027,111,358,279.
(1)在以上模拟的20组数中,随机抽取3组数,至少有1组获奖的概率;
(2)根据以上模拟试验的结果,将频率视为概率:
(ⅰ)若活动期间某单位购买四台电视,求恰好有两台获奖的概率;
(ⅱ)若本次活动平均每台电视的奖金不超过260元,求m的最大值.
(1)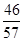 ;(2)(ⅰ)
;(2)(ⅰ) ,(ⅱ)400.
,(ⅱ)400.
解析试题分析:解题思路:(1)利用对立事件的概率与古典概型的概率公式求解即可;(2)(ⅰ)根据二项分布的概率公式求解;(ⅱ)平均奖金即随机奖金的数学期望.规律总结:1.遇到“至少”、“至多”,且正面情况较多时,可以考虑对立事件的概率;2.利用概率或随机变量的分布列以及期望、方差解决应用题时,要注意随机变量的实际意义.
试题解析:(1)在20组数中,获奖的数组有8组,
记“至少有1组获奖”为事件A,则 .
.
(2)(ⅰ)购买一台电视机获奖的概率为 ,
,
则购买的四台电视恰好有两台获奖的概率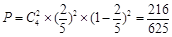 .
.
(ⅱ)记每台电视的奖金为随机变量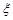 ,则
,则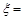 0,m,2m,5m.
0,m,2m,5m.
由题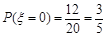 ;
; ;
;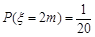 ;
;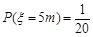 .
.
则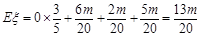 ,
,
由于平均每台电视的奖金不超过260元,
所以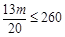 ,解得
,解得 ,
,
故本次活动平均每台电视的奖金不超过260元时,m的最大值是400元.
考点:1.古典概型;2.二项分布;3.随机变量的数学期望.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为
 .(12分)
.(12分)(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为
 ,求
,求 的分布列与期望.
的分布列与期望.下面的临界值表供参考:
 | 0.15 | 0.10 | 0.05[ | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:
 ,其中
,其中 )
)
 (已知甲回答每道题的正确率相同,并且相互之间没有影响).
(已知甲回答每道题的正确率相同,并且相互之间没有影响). .
.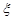 的数学期望和方差.
的数学期望和方差.
 、
、 两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为
两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为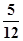 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为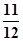 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品. 个,设
个,设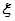 表示其中合格品的个数,求
表示其中合格品的个数,求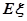 .
.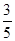 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是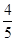 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用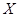 表示张同学答对题的个数,求
表示张同学答对题的个数,求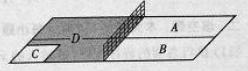 甲上有两个不相交的区域
甲上有两个不相交的区域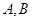 ,乙被划分为两个不相交的区域
,乙被划分为两个不相交的区域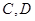 .某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在
.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在 上记3分,在
上记3分,在 上记1分,其它情况记0分.对落点在
上记1分,其它情况记0分.对落点在 上的来球,队员小明回球的落点在
上的来球,队员小明回球的落点在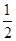 ,在
,在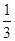 ;对落点在
;对落点在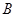 上的来球,小明回球的落点在
上的来球,小明回球的落点在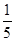 ,在
,在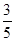 .假设共有两次来球且落在
.假设共有两次来球且落在 的分布列与数学期望.
的分布列与数学期望.