题目内容
某地区为了解高二学生作业量和玩电脑游戏的情况,对该地区内所有高二学生采用随机抽样的方法,得到一个容量为200的样本.统计数据如下:
(1)已知该地区共有高二学生42500名,根据该样本估计总体,其中喜欢电脑游戏并认为作业不多的人有多少名?
(2)在A,B,C,D,E,F六名学生中,仅有A,B两名学生认为作业多.如果从这六名学生中随机抽取两名,求至少有一名学生认为作业多的概率.
(1)7650名;(2)
解析试题分析:(1)利用样本估计总体,可求得喜欢电脑游戏并认为作业不多的人数;(2)用列举法,并利用古典概型即可求得至少有一名学生认为作业多的概率
试题解析:(1)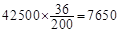 (名) 5分
(名) 5分
(2)【方法一】从这六名学生中随机抽取两名的基本事件有:{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},{C,D},{C,E},{C,F},{D,E},{D,F},{E,F}共15个 7分
其中至少有一个学生认为作业多的事件有{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F}共9个 9分
∴
即至少有一名学生认为作业多的概率为 . 12分
. 12分
【方法二】6名学生中随机抽取2名的选法有 种, 7分
种, 7分
其中至少有一名学生认为作业多的选法有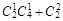 =9种, 9分
=9种, 9分
∴
即至少有一名学生认为作业多的概率为 . 12分
. 12分
【方法三】6名学生中随机抽取2名的选法有 种, 7分
种, 7分
其中没有人认为作业多的选法有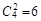 种 9分
种 9分
∴
即至少有一名学生认为作业多的概率为 . 12分
. 12分
考点:统计,随机抽样,用样本估计总体,古典概型.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案某校夏令营有3名男同学 和3名女同学
和3名女同学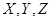 ,其年级情况如下表:
,其年级情况如下表:
| | 一年级 | 二年级 | 三年级 |
| 男同学 |  | 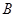 | 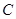 |
| 女同学 | 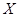 | 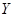 | 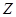 |
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同)
(1)用表中字母列举出所有可能的结果
(2)设
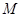 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件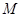 发生的概率.
发生的概率. 为了解某班学生关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合 计 |
| 男 生 | | 6 | |
| 女 生 | 10 | | |
| 合 计 | | | 48 |
已知在全班48人中随机抽取1人,抽到关注NBA的学生的概率为2/3
⑴请将上面列连表补充完整,并判断是否有
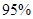 的把握认为关注NBA与性别有关?
的把握认为关注NBA与性别有关?⑵现从女生中抽取2人进一步调查,设其中关注NBA的女生人数为X,求X的分布列与数学期望.
附:
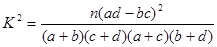 ,其中
,其中 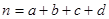
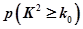 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
某家电专卖店在五一期间设计一项有奖促销活动,每购买一台电视,即可通过电脑产生一组3个数的随机数组,根据下表兑奖:
| 奖次 | 一等奖 | 二等奖 | 三等奖 |
| 随机数组的特征 | 3个1或3个0 | 只有2个1或2个0 | 只有1个1或1个0 |
| 资金(单位:元) | 5m | 2m | m |
商家为了了解计划的可行性,估计奖金数,进行了随机模拟试验,并产生了20个随机数组,试验结果如下:
247,235,145,124,754,353,296,065,379,118,520,378,218,953,254,368,027,111,358,279.
(1)在以上模拟的20组数中,随机抽取3组数,至少有1组获奖的概率;
(2)根据以上模拟试验的结果,将频率视为概率:
(ⅰ)若活动期间某单位购买四台电视,求恰好有两台获奖的概率;
(ⅱ)若本次活动平均每台电视的奖金不超过260元,求m的最大值.
小王经营一家面包店,每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元,若当天卖不完,则未卖出的现烤面包因过期每个亏损5元.经统计,得到在某月(30天)中,小王每天售出的现烤面包个数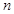 及天数如下表:
及天数如下表:
售出个数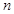 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天数 | 3 | 3 | 3 | 6 | 9 | 6 |
(1)计算小王某天售出该现烤面包超过13个的概率;
(2)若在今后的连续5天中,售出该现烤面包超过13个的天数大于3天,则小王决定增加订购量.试求小王增加订购量的概率.
(3)若小王每天订购14个该现烤面包,求其一天出售该现烤面包所获利润的分布列和数学期望.
 为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为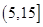 ,
,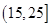 ,
,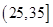 ,
,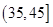 ,由此得到样本的空气质量指数频率分布直方图,如图.
,由此得到样本的空气质量指数频率分布直方图,如图.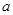 的值;
的值; 组的频率为
组的频率为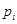 ,第
,第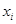
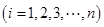 ,则样本数据的平均值为
,则样本数据的平均值为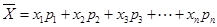 .)
.) ,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取
,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取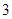 天的数值,其中达到“特优等级”的天数为
天的数值,其中达到“特优等级”的天数为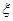 ,求
,求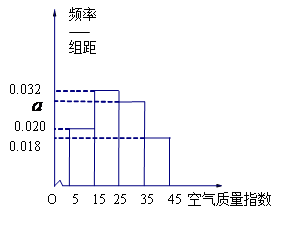
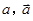 分别表示甲组研发成功和失败;
分别表示甲组研发成功和失败;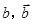 分别表示乙组研发成功和失败.
分别表示乙组研发成功和失败.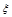 表示取到次品的个数,则E
表示取到次品的个数,则E