题目内容
已知函数f(x)=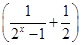 x3.
x3.
(1)判断f(x)的奇偶性;(2)求证:f(x)>0.
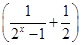 x3.
x3.(1)判断f(x)的奇偶性;(2)求证:f(x)>0.
(1)偶函数(2)见解析
(1)解 ∵2x-1≠0,∴函数f(x)的定义域为{x|x≠0}.
∵f(-x)-f(x)=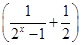 (-x)3-
(-x)3-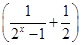 x3
x3
=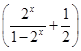 (-x)3-
(-x)3-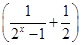 x3
x3
=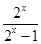 ·x3-
·x3- x3-
x3- ·x3-
·x3- x3=x3-x3=0,
x3=x3-x3=0,
∴f(-x)=f(x),∴f(x)是偶函数.
(2)证明 由题意知x≠0,
当x>0时,∵2x-1>0,x3>0,∴f(x)>0;
当x<0时,∵-x>0,∴f(-x)=f(x)>0,
∴f(x)>0.综上所述,f(x)>0.
∵f(-x)-f(x)=
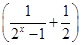 (-x)3-
(-x)3-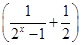 x3
x3=
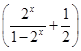 (-x)3-
(-x)3-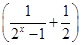 x3
x3=
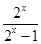 ·x3-
·x3- x3-
x3- ·x3-
·x3- x3=x3-x3=0,
x3=x3-x3=0,∴f(-x)=f(x),∴f(x)是偶函数.
(2)证明 由题意知x≠0,
当x>0时,∵2x-1>0,x3>0,∴f(x)>0;
当x<0时,∵-x>0,∴f(-x)=f(x)>0,
∴f(x)>0.综上所述,f(x)>0.

练习册系列答案
相关题目
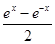 ,x∈R
,x∈R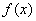 是定义在实数集
是定义在实数集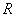 上的以2为周期的偶函数,当
上的以2为周期的偶函数,当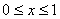 时,
时,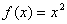 .若直线
.若直线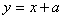 与函数
与函数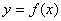 的图像在
的图像在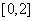 内恰有两个不同的公共点,则实数
内恰有两个不同的公共点,则实数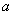 的值是( )
的值是( ) 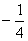 或
或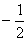 ;
;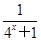 是奇函数,则常数a=________.
是奇函数,则常数a=________.