题目内容
已知函数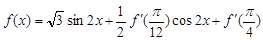 .
.
(1)求 的最小正周期和最小值;
的最小正周期和最小值;
(2)若不等式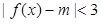 对任意
对任意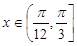 恒成立,求实数
恒成立,求实数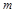 的取值范围.
的取值范围.
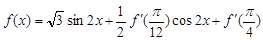 .
.(1)求
 的最小正周期和最小值;
的最小正周期和最小值;(2)若不等式
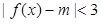 对任意
对任意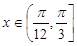 恒成立,求实数
恒成立,求实数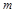 的取值范围.
的取值范围.(1)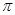 ,
,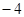 ;(2)
;(2)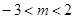 .
.
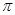 ,
,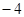 ;(2)
;(2)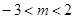 .
.试题分析:(1)由于函数
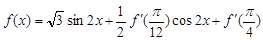 中含有常数
中含有常数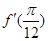 ,
,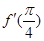 ,先求
,先求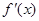 ,再令
,再令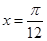 ,
,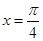 ,分别求出
,分别求出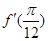 ,
,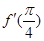 ,再利用两个角的和的正弦公式变形为
,再利用两个角的和的正弦公式变形为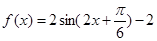 ,即可求得最小正正周期与最值;(2)当
,即可求得最小正正周期与最值;(2)当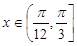 时,利用(1)的结论求得
时,利用(1)的结论求得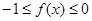 ,
,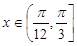 时不等式
时不等式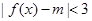 恒成立等价于
恒成立等价于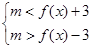 在
在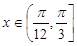 时恒成立.
时恒成立.试题解析:(1)
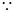
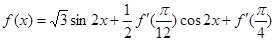 ,
,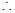
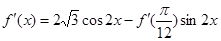 ,
,令
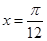 得
得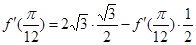 ,解得
,解得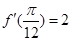 ,
,
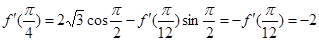 ,
,
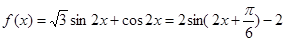 .
.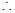 最小正周期
最小正周期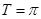 ,最小值为
,最小值为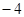 . 6分
. 6分 (2)有(1)知
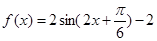 ,当
,当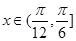 时
时 ,
,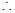
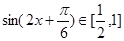 ,则
,则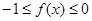 , 8分
, 8分 又对任意
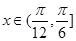 ,
,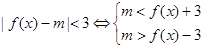 恒成立.
恒成立.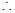
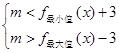 ,即
,即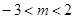 . 12分
. 12分 
练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
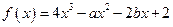 处有极值,则ab的最大值等于( ).
处有极值,则ab的最大值等于( ).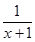
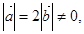 且关于
且关于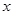 的函数
的函数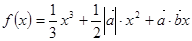 在
在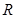 上有极值,则
上有极值,则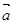 与
与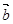 的夹角范围是( )
的夹角范围是( )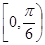

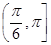

 的最大值____________.
的最大值____________.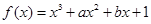 的导数
的导数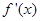 满足
满足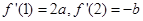 ,其中
,其中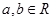 .
.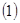 求曲线
求曲线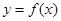 在点
在点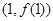 处的切线方程;
处的切线方程;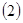 设
设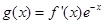 ,求函数
,求函数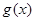 的极值.
的极值.