题目内容
6.设函数f(x)=(a-x)ex-1(e为自然对数的底数).(Ⅰ)当a=1时,求f(x)的最大值;
(Ⅱ)当x∈(-∞,0)∪(0,+∞)时,$\frac{f(x)}{x}$<1恒成立,证明:a=1.
分析 (Ⅰ)求出当a=1时,函数f(x)的导数,求得增区间和减区间,即可得到极大值,即为最大值f(0);
(Ⅱ)①当x∈(-∞,0)时,$\frac{f(x)}{x}$<1?(a-x)ex>x+1即a>x+$\frac{x+1}{{e}^{x}}$,②当x∈(0,+∞)时,$\frac{f(x)}{x}$<1?(a-x)ex<x+1,a<x+$\frac{x+1}{{e}^{x}}$,分别求出右边函数的最值或值域,即可得证a=1.
解答 解:(Ⅰ)当a=1时,f′(x)=-ex+(1-x)ex=-xex.
当x>0时,f′(x)<0,f(x)在(0,+∞)上单调递减;
当x<0时,f′(x)>0,f(x)在(-∞,0)上单调递增.
故f(x)在x=0处取得极大值,也为最大值f(0)=0.
(Ⅱ)证明:①当x∈(-∞,0)时,$\frac{f(x)}{x}$<1?(a-x)ex>x+1即a>x+$\frac{x+1}{{e}^{x}}$,
令g(x)=x+$\frac{x+1}{{e}^{x}}$,g′(x)=1-$\frac{x}{{e}^{x}}$>0,
则g(x)在(-∞,0)上是增函数,g(x)<g(0)=1,即有a≥1.
②当x∈(0,+∞)时,$\frac{f(x)}{x}$<1?(a-x)ex<x+1,a<x+$\frac{x+1}{{e}^{x}}$,由①知g′(x)=$\frac{{e}^{x}-x}{{e}^{x}}$,
令h(x)=ex-x,h′(x)=ex-1>0,
则h(x)>h(0)=1,g′(x)>0,g(x)>g(0)=1,即有a≤1.
故a=1.
点评 本题考查导数的运用:求单调区间和极值、最值,主要考查函数的单调性的运用,同时考查不等式恒成立思想的运用,属于中档题.

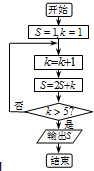
| A. | 57 | B. | 119 | C. | 120 | D. | 247 |

| A. | 17 | B. | 29 | C. | 44 | D. | 52 |