题目内容
9.已知g(x)=bx2+cx+1,f(x)=x2+ax-lnx+1,g(x)在x=1处的切线为y=2x(Ⅰ)求b,c的值;
(Ⅱ)若a=-1,求f(x)的极值;
(Ⅲ)设h(x)=f(x)-g(x),是否存在实数a,当x∈(0,e],(e≈2.718,为自然常数)时,函数h(x)的最小值为3.
分析 (Ⅰ)求出函数g(x)的导数,求得切线的斜率,由已知切线方程,可得2b+c=2,b+c+1=2,解得b,c即可;
(Ⅱ)求出f(x)的导数,令导数大于0,得增区间,令导数小于0,得减区间,即可得到极值;
(Ⅲ)求出h(x)的导数,讨论①当a≤0时,②当0<a≤$\frac{1}{e}$时,当a>$\frac{1}{e}$,通过单调性判断函数的最值情况,即可判断是否存在.
解答 解:(1)g(x)=bx2+cx+1的导数为g′(x)=2bx+c,
g(x)在x=1处的切线斜率为2b+c,
由g(x)在x=1处的切线为y=2x,
则2b+c=2,b+c+1=2,
解得b=1,c=0;
(Ⅱ)若a=-1,则f(x)=x2-x-lnx+1,定义域为(0,+∞),
∴f′(x)=2x-1-$\frac{1}{x}$=$\frac{2{x}^{2}-x-1}{x}$=$\frac{(x-1)(2x+1)}{x}$,
令f′(x)=0,解得x=1,
当x>1,f′(x)>0,f(x)递增;
当0<x<1时,f′(x)<0,f(x)递减.
即有x=1处,f(x)取得极小值,且为f(x)极小=f(1)=1,
(Ⅲ)h(x)=f(x)-g(x)=x2+ax-lnx+1-(x2+1)=ax-lnx,
假设存在实数a,使h(x)=ax-lnx,x∈(0,e],h有最小值3,
h′(x)=a-$\frac{1}{x}$,
①当a≤0时,h′(x)<0,
∴h(x)在(0,e]上单调递减,h(x)min=h(e)=ae-1=3,解得a=$\frac{4}{e}$(舍去),
②当a>0时,h′(x)=a-$\frac{1}{x}$=$\frac{a(x-\frac{1}{x})}{x}$,
(i)当0<a≤$\frac{1}{e}$时,$\frac{1}{a}$≥e,h′(x)<0在(0,e]上恒成立,
所以(x)在(0,e]上单调递减,h(x)min=h(e)=ae-1=3,解得a=$\frac{4}{e}$(舍去),
(ii)当a>$\frac{1}{e}$时,0<$\frac{1}{a}$<e,当0<x<$\frac{1}{a}$时,h′(x)<0,所以h(x)在(0,$\frac{1}{a}$)上递减,
当$\frac{1}{a}$<x<e时,h′(x)>0,h(x)在($\frac{1}{a}$,e)上递增,
所以,h(x)min=h($\frac{1}{a}$)=1+lna=3,
所以a=e2满足条件,
综上,存在a=e2使当x∈(0,e],(e≈2.718,为自然常数)时,函数h(x)的最小值为3.
点评 本题考查导数的运用:求切线方程和单调区间、极值和最值,同时考查存在性问题的解法,考查运算能力,属于中档题.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案| A. | 1+i或-2+i | B. | i或1+i | C. | i或-1+i | D. | -1-i或-2+i |
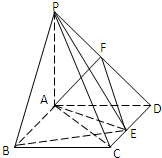 如图,在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点F是PD的中点,点E在CD上移动.
如图,在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点F是PD的中点,点E在CD上移动.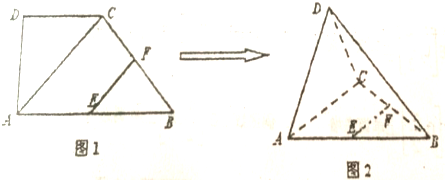
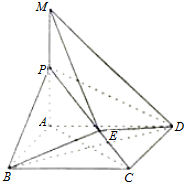
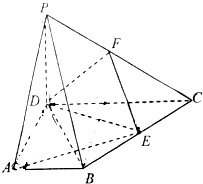 如图,四棱锥P-ABCD的底面是直角梯形,∠BAD=∠CDA=90°,侧面PAD⊥底面ABCD,AB=PD=1,PA=DC=2,AD=$\sqrt{3}$,点E是BC的中点.
如图,四棱锥P-ABCD的底面是直角梯形,∠BAD=∠CDA=90°,侧面PAD⊥底面ABCD,AB=PD=1,PA=DC=2,AD=$\sqrt{3}$,点E是BC的中点.