题目内容
17.已知函数f(x)=$\frac{1}{2}a{x^2}$-bx,g(x)=lnx-f(x).(Ⅰ)若f(2)=2,讨论函数g(x)的单调性;
(Ⅱ)若f(x)是关于x的一次函数,且函数g(x)有两个不同的零点x1,x2,求实数b的取值范围;
(Ⅲ)在(Ⅱ)的条件下,求证:x1x2>e2.
分析 (Ⅰ)先求出g(x)的导数,通过讨论a的范围,得到函数g(x)的单调性;
(Ⅱ)由f(x)=-bx,得到g(x)的表达式,令g(x)=0,得$b=-\frac{lnx}{x}$,记$h(x)=-\frac{lnx}{x}$,通过讨论h(x)的单调性,得到h(x)取得最小值$-\frac{1}{e}$,从而得到b的范围;
(Ⅲ)要证${x_1}{x_2}>{e^2}$,即证$ln\frac{x_2}{x_1}>\frac{{2({x_2}-{x_1})}}{{{x_1}+{x_2}}}=\frac{{2(\frac{x_2}{x_1}-1)}}{{1+\frac{x_2}{x_1}}}$,设$t=\frac{x_2}{x_1}$(t>1),$F(t)=lnt-\frac{2(t-1)}{1+t}=lnt+\frac{4}{t+1}-2$,通过求导得到F(t)的单调性,从而得到F(t)>0,进而证出结论.
解答 解:(Ⅰ)由f(2)=2,得a-b=1.
则$g(x)=lnx-\frac{1}{2}a{x^2}+(a-1)x$,其定义域为(0,+∞),
$g'(x)=\frac{1}{x}-ax+(a-1)=\frac{{-a{x^2}+(a-1)x+1}}{x}=-\frac{(ax+1)(x-1)}{x}$,
当a<0时,令g'(x)=0,解得${x_1}=-\frac{1}{a}$,x2=1,
①当a<-1时,则$0<-\frac{1}{a}<1$,
函数g(x)在区间$(0{,_{\;}}-\frac{1}{a})$和(1,+∞)上单调递增,
在区间$(-\frac{1}{a}{,_{\;}}1)$上单调递减,
②当a=-1时,$g'(x)=\frac{{{{(x-1)}^2}}}{x}$≥0,
函数g(x)在区间(0,+∞)上单调递增,
③当-1<a<0时,则$-\frac{1}{a}>1$,
函数g(x)在区间(0,1)和$(-\frac{1}{a}{,_{\;}}+∞)$上单调递增,
在区间$(1{,_{\;}}-\frac{1}{a})$上单调递减,
④当a≥0时,g(x)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减,
(Ⅱ)∵f(x)是关于x的一次函数,
∴g(x)=lnx+bx,其定义域为(0,+∞).
由g(x)=0,得$b=-\frac{lnx}{x}$,记$h(x)=-\frac{lnx}{x}$,则$h'(x)=\frac{lnx-1}{x^2}$,
∴$h(x)=-\frac{lnx}{x}$在(0,e)上单调递减,在(e,+∞)上单调递增.
∴当x=e时,$h(x)=-\frac{lnx}{x}$取得最小值$-\frac{1}{e}$,
由h(1)=0,得x∈(0,1)时,h(x)>0,
而x∈(1,+∞)时,h(x)<0,如下图: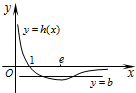
∴实数b的取值范围是$(-\frac{1}{e}{,_{\;}}0)$.
(Ⅲ)由题意,得lnx1+bx1=0,lnx2+bx2=0,
故lnx1x2+b(x1+x2)=0,$ln\frac{x_2}{x_1}+b({x_2}-{x_1})=0$.
∴$\frac{{ln{x_1}{x_2}}}{{ln\frac{x_2}{x_1}}}=\frac{{{x_1}+{x_2}}}{{{x_2}-{x_1}}}$.
不妨设x1<x2,要证${x_1}{x_2}>{e^2}$,只需证$ln{x_1}{x_2}=\frac{{{x_1}+{x_2}}}{{{x_2}-{x_1}}}•ln\frac{x_2}{x_1}>2$,
即证$ln\frac{x_2}{x_1}>\frac{{2({x_2}-{x_1})}}{{{x_1}+{x_2}}}=\frac{{2(\frac{x_2}{x_1}-1)}}{{1+\frac{x_2}{x_1}}}$,
设$t=\frac{x_2}{x_1}$(t>1),$F(t)=lnt-\frac{2(t-1)}{1+t}=lnt+\frac{4}{t+1}-2$,
则$F'(t)=\frac{1}{t}-\frac{4}{{{{(t+1)}^2}}}=\frac{{{{(t-1)}^2}}}{{t{{(t+1)}^2}}}>0$,
∴函数F(t)在(1,+∞)上单调递增,而F(1)=0.
∴F(t)>0,即$lnt>\frac{2(t-1)}{1+t}$.
∴${x_1}{x_2}>{e^2}$.
点评 本题考察了导数的应用,考察函数的单调性、函数的极值问题,考察分类讨论思想、换元思想,本题是一道难题.

| A. | 57 | B. | 119 | C. | 120 | D. | 247 |
| A. | 1+i或-2+i | B. | i或1+i | C. | i或-1+i | D. | -1-i或-2+i |
 在以棱长为1的正方形ABCD-A1B1C1D1中,求:
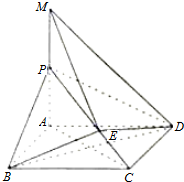
在以棱长为1的正方形ABCD-A1B1C1D1中,求: 如图,在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点F是PD的中点,点E在CD上移动.
如图,在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点F是PD的中点,点E在CD上移动.