题目内容
20．已知向量$\overrightarrow{AB}$=（-3，a），$\overrightarrow{AC}$=（1-a，2），若A，B，C三点共线，则a=（ ）| A． | 3或-2 | B． | 2或-3 | C． | $\frac{3}{5}$ | D． | 3 |
分析 向量共线，即向量平行，即可得到a（1-a）=-3×2，解得即可．
解答 解：若A，B，C三点共线，向量$\overrightarrow{AB}$=（-3，a），$\overrightarrow{AC}$=（1-a，2），
∴a（1-a）=-3×2，
即a2-a-6=0
解得a=3或a=-2，
故选：A．
点评 本题考查了向量的共线的条件，以及向量共线的坐标运算，属于基础题．
练习册系列答案
相关题目
10．若$\overrightarrow{AB}$=3$\overrightarrow{a}$，$\overrightarrow{CD}$=-5$\overrightarrow{a}$，且|$\overrightarrow{AD}$|=|$\overrightarrow{BC}$|，则四边形ABCD是（ ）
| A． | 平行四边形 | B． | 菱形 | C． | 等腰梯形 | D． | 不等腰梯形 |
11．如图程序框图输出的结果为（ ）
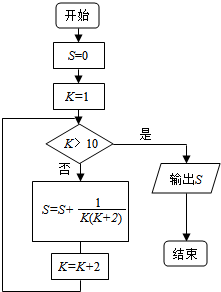
| A． | $\frac{5}{11}$ | B． | $\frac{5}{13}$ | C． | $\frac{4}{9}$ | D． | $\frac{6}{13}$ |
如图所示，在长方体OABC-O1A1B1C1中，|OA|=2，|AB|=3，|AA1|=3，M是OB1与BO1的交点，则M点的坐标是$（1，\frac{3}{2}，\frac{3}{2}）$．
5．△ABC的外接圆的圆心为O，半径为1，若$\overrightarrow{AB}$+$\overrightarrow{AC}$=2$\overrightarrow{AO}$，且|$\overrightarrow{OA}$|=|$\overrightarrow{AC}$|，则△ABC的面积为（ ）
| A． | $\sqrt{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | 2$\sqrt{3}$ | D． | 1 |
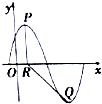已知函数f（x）=Asin（$\frac{π}{3}x$+φ），（A＞0，0＜φ＜$\frac{π}{2}$），y=f（x）的部分图象如图所示，P，Q分别为该图象上相邻的最高点和最低点，点P在x轴上的射影为R（1，0），cos∠PRQ=-$\frac{4}{5}$．