题目内容
4.具有线性相关关系的变量x,y,满足一组数据如下表所示:| X | 0 | 1 | 2 | 3 |
| y | -1 | 1 | m | 8 |
分析 利用平均数公式计算预报中心点的坐标,根据回归直线必过样本的中心点可得答案.
解答 解:由题意,$\overline{x}$=1.5,$\overline{y}$=$\frac{8+m}{4}$,
∴样本中心点是坐标为(1.5,$\frac{8+m}{4}$),
∵回归直线必过样本中心点,y与x的回归直线方程为$\widehat{y}$=3x-$\frac{3}{2}$,
∴$\frac{8+m}{4}$=3×1.5-1.5,
∴m=4
故答案为:4.
点评 本题考查了线性回归直线的性质,回归直线必过样本的中心点.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
9.根据下面一组等式
S1=1,
S2=2+3=5,
S3=4+5+6=15,
S4=7+8+9+10=34,
S5=11+12+13+14+15=65,
S6=16+17+18+19+20+21=111,
S7=22+23+24+25+26+27+28=175,
…
可得S1+S3+S5+…+S2n-1=( )
S1=1,
S2=2+3=5,
S3=4+5+6=15,
S4=7+8+9+10=34,
S5=11+12+13+14+15=65,
S6=16+17+18+19+20+21=111,
S7=22+23+24+25+26+27+28=175,
…
可得S1+S3+S5+…+S2n-1=( )
| A. | 2n2 | B. | n3 | C. | 2n3 | D. | n4 |
16.${∫}_{0}^{1}$(2x+2)dx=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
13.抛掷质地均匀的甲、乙两颗骰子,设出现的点数分别为a、b,则满足$\frac{a}{2}$<|b-a2|<6-a的概率为( )
| A. | $\frac{13}{36}$ | B. | $\frac{5}{18}$ | C. | $\frac{7}{36}$ | D. | $\frac{5}{36}$ |
 如图所示,在长方体OABC-O1A1B1C1中,|OA|=2,|AB|=3,|AA1|=3,M是OB1与BO1的交点,则M点的坐标是$(1,\frac{3}{2},\frac{3}{2})$.
如图所示,在长方体OABC-O1A1B1C1中,|OA|=2,|AB|=3,|AA1|=3,M是OB1与BO1的交点,则M点的坐标是$(1,\frac{3}{2},\frac{3}{2})$.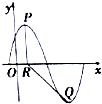 已知函数f(x)=Asin($\frac{π}{3}x$+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$.
已知函数f(x)=Asin($\frac{π}{3}x$+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$.