题目内容
【题目】已知O为坐标原点,椭圆C:![]() 的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,若|OB|,|OF2|,|AB|成等比数列,椭圆C上的点到焦点F2的最短距离为
的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,若|OB|,|OF2|,|AB|成等比数列,椭圆C上的点到焦点F2的最短距离为![]() .
.
(1)求椭圆C的标准方程;
(2)设T为直线x=-3上任意一点,过F1的直线交椭圆C于点P,Q,且![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】
⑴利用已知条件,算出![]() ,
,![]() ,再根据
,再根据![]() ,求出
,求出![]() ,写出椭圆方程
,写出椭圆方程
⑵![]() 可得
可得![]() ,设
,设![]() ,直线
,直线![]() 的方程为
的方程为![]() ,联立直线
,联立直线![]() 的方程和椭圆
的方程和椭圆![]() 的方程,消去
的方程,消去![]() ,根据韦达定理,求出
,根据韦达定理,求出![]() 的表达式,利用基本不等式求出最小值
的表达式,利用基本不等式求出最小值
解:(1)易知![]() ,
,![]() ,
,![]()
而![]() 又
又![]() ,得
,得![]() ,
,
故椭圆![]() 的标准方程为
的标准方程为![]()
(2)由(1)知![]() ,∵
,∵![]() ,故
,故![]() ,设
,设![]() ,
,
∴![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
当![]() 时,直线
时,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的方程为
的方程为![]() ;
;
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,也符合方程
,也符合方程![]() .
.
设![]() ,
,![]() ,将直线
,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立,得
的方程联立,得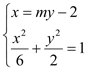
消去![]() ,得:
,得:![]() ,
,![]() ,
,![]() ,
,![]()
![]()
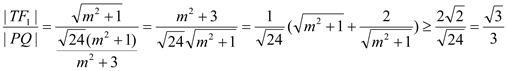
当且仅当![]() ,即
,即![]() 时,等号成立.
时,等号成立.
∴![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
相关题目
