题目内容
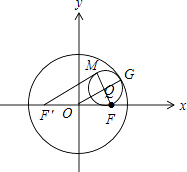
【题目】已知圆O:x2+y2=4,点F( ![]() ,0),以线段MF为直径的圆内切于圆O,记点M的轨迹为C
,0),以线段MF为直径的圆内切于圆O,记点M的轨迹为C
(1)求曲线C的方程;
(2)若过F的直线l与曲线C交于A,B两点,问:在x轴上是否存在点N,使得 ![]() 为定值?若存在,求出点N坐标;若不存在,说明理由.
为定值?若存在,求出点N坐标;若不存在,说明理由.
【答案】
(1)解:设FM的中点为Q,切点为G,连OQ,QG,
则|OQ|+|QG|=|OG|=2,取F关于y轴的对称点F′,连F′M,
故|F′M|+|MF|=2(|OQ|+|QG|)=4.
点M的轨迹是以F′,F为焦点,长轴长为4的椭圆.
其中,a=2,c=,b=1,则曲线C的方程为 ![]() +y2=1
+y2=1
(2)解:当直线l的斜率存在时,设其方程为y=k(x﹣ ![]() ),
),
A(x1,y1),B(x2,y2),
联立 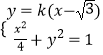 ,得
,得 ![]() .
.
则△>0, ![]() ,
,
若存在定点N(m,0)满足条件,
则有 ![]() =(x1﹣m)(x2﹣m)+y1y2
=(x1﹣m)(x2﹣m)+y1y2
=x1x2+ ![]()
= ![]()
= ![]() =
= ![]() .
.
如果要上式为定值,则必须有 ![]() ,解得m=
,解得m= ![]() ,
,
此时 ![]() =
= ![]() .
.
验证当直线l斜率不存在时,也符合.
故存在点N( ![]() ,0)满足
,0)满足 ![]() 为定值.
为定值.
【解析】(1)设FM的中点为Q,切点为G,连OQ,QG,通过|OQ|+|QG|=|OG|=2,推出|F′M|+|MF|=4.说明点M的轨迹是以F′,F为焦点,长轴长为4的椭圆.然后求解曲线C的方程;(2)当直线l的斜率存在时,设其方程为y=k(x﹣ ![]() ),联立直线方程和椭圆方程,利用根与系数的关系得到A,B的横坐标的和与积,代入
),联立直线方程和椭圆方程,利用根与系数的关系得到A,B的横坐标的和与积,代入 ![]() ,由
,由 ![]() 为定值求得m值,验证斜率不存在时适合得答案.
为定值求得m值,验证斜率不存在时适合得答案.

练习册系列答案
相关题目