题目内容
【题目】函数![]() 满足如下四个条件:
满足如下四个条件:
①定义域为![]() ;
;
②![]() ;
;
③当![]() 时,
时,![]() ;
;
④对任意![]() 满足
满足![]() .
.
根据上述条件,求解下列问题:
⑴求![]() 及
及![]() 的值.
的值.
⑵应用函数单调性的定义判断并证明![]() 的单调性.
的单调性.
⑶求不等式![]() 的解集.
的解集.
【答案】(1)0; (2)见解析; (3) ![]()
【解析】
(1) 在![]() 中,令
中,令![]() 可得:
可得:![]() ;
;
在![]() 中,令
中,令![]() ,可得
,可得![]() .
.
(2)![]() 为
为![]() 上的增函数.设
上的增函数.设![]() ,利用,
,利用,![]() ,
,
可得![]()
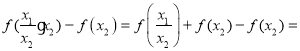
![]() ,结合
,结合![]() 时,
时,![]() ,利用单调性的定义可证.
,利用单调性的定义可证.
(3)根据![]() ,可得
,可得![]() ,所以原不等式可化为
,所以原不等式可化为![]()
![]()
![]() ,再利用单调性可解得.
,再利用单调性可解得.
(1)在![]() 中,
中,
令![]() ,得
,得![]() ,解得
,解得![]() .
.
在![]() 中,令
中,令![]() .
.
得![]() ,
,
得![]() ,
,
得![]() ,
,
所以![]() .
.
(2) ![]() 为
为![]() 上的增函数.
上的增函数.
证明如下:设![]() ,则
,则![]() 所以
所以![]() .
.
因为![]() =
=![]() =
=![]()
![]() ,
,
即![]() .
.
根据增函数的定义可知, ![]() 为
为![]() 上的增函数.
上的增函数.
(3)因为![]() ,
,
所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
所以![]()
![]() ,
,
所以![]()
![]() ,
,
由(2)知函数![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,解得:
,解得:![]() .
.
所以不等式![]() 的解集是
的解集是![]() .
.

练习册系列答案
相关题目