题目内容
【题目】如图，DOAB是边长为2的正三角形，当一条垂直于底边OA（垂足不与O，A重合）的直线x=t从左至右移动时，直线l把三角形分成两部分，记直线l左边部分的面积y．
（Ⅰ）写出函数y= f（t）的解析式；
（Ⅱ）写出函数y= f（t）的定义域和值域．
【答案】（1） 见解析（2）见解析
【解析】
试题（1） 由题易知，当t在B左侧时（即0＜t≤1）直线l左边部分为三角形，面积可表示为
当t在B右侧时（即1＜t＜2）直线l左边部分图形不规则，可化为用三角形OAB面积减去剩下的三角形的面积即：
（2）由（1）联系问题的具体情况易求出定义域及值域。
试题解析： （1） 当0＜t≤1时，y=
当1＜t＜2时，y=
所以，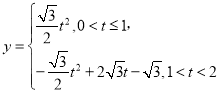
（2）由题知，y=f（x）的定义域为（0,2）， 由问题的实际意义知，y=f（x）的值域为（0,
）.
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
