Question

【题目】定义在R上的奇函数y=f（x）满足f（3）=0，且当x＞0时，不等式f（x）＞﹣xf′（x）恒成立，则函数g（x）=xf（x）+lg|x+1|的零点的个数为（ ）
A.1
B.2
C.3
D.4

Answer 1

【答案】C
【解析】解：定义在R的奇函数f（x）满足：
f（0）=0=f（3）=f（﹣3），
且f（﹣x）=﹣f（x），
又x＞0时，f（x）＞﹣xf′（x），即f（x）+xf′（x）＞0，
∴[xf（x）]'＞0，函数h（x）=xf（x）在x＞0时是增函数，
又h（﹣x）=﹣xf（﹣x）=xf（x），∴h（x）=xf（x）是偶函数；
∴x＜0时，h（x）是减函数，结合函数的定义域为R，且f（0）=f（3）=f（﹣3）=0，
可得函数y1=xf（x）与y2=﹣lg|x+1|的大致图象如图所示，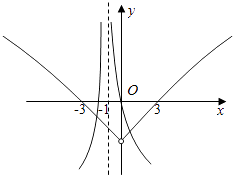

∴由图象知，函数g（x）=xf（x）+lg|x+1|的零点的个数为3个．
故选：C．
由不等式f（x）＞﹣xf′（x）在（0，+∞）上恒成立，得到函数h（x）=xf（x）在x＞0时是增函数，
再由函数y=f（x）是定义在R上的奇函数得到h（x）=xf（x）为偶函数，
结合f（0）=f（3）=f（﹣3）=0，作出两个函数y1=xf（x）与y2=﹣lg|x+1|的大致图象，即可得出答案．