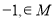题目内容
2.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的上顶点为(0,1),且离心率为$\frac{\sqrt{3}}{2}$.(Ⅰ)求椭圆C的方程;
(Ⅱ)证明:过椭圆C1:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)上一点Q(x0,y0)的切线方程为$\frac{{x}_{0}x}{{m}^{2}}$+$\frac{{y}_{0}y}{{n}^{2}}$=1;
(Ⅲ)过圆x2+y2=16上一点P向椭圆C引两条切线,切点分别为A,B,当直线AB分别与x轴、y轴交于M,N两点时,求|MN|的最小值.
分析 (Ⅰ)运用离心率公式和椭圆的a,b,c的关系,解得a,b,进而得到椭圆方程;
(Ⅱ)讨论直线的斜率不存在和存在,设出直线方程,联立椭圆方程,运用判别式为0,解得方程的一个跟,得到切点坐标和切线的斜率,进而得到切线方程;
(Ⅲ)设点P(xP,yP)为圆x2+y2=16上一点,求得切线PA,PB的方程,进而得到切点弦方程,再由两点的距离公式可得|MN|,结合基本不等式,即可得到最小值.
解答 解:(Ⅰ)由题意可得b=1,e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
又a2-b2=c2,解得a=2,b=1,
即有椭圆C方程为$\frac{{x}^{2}}{4}$+y2=1.
(Ⅱ)证明:当斜率存在时,设切线方程为y=kx+t,联立椭圆方程$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1,
可得n2x2+m2(kx+t)2=m2n2,化简可得:
(n2+m2k2)x2+2m2ktx+m2(t2-n2)=0,①
由题可得:△=4m4k2t2-4m2(n2+m2k2)(t2-n2)=0
化简可得:t2=m2k2+n2,①式只有一个根,记作x0,
x0=-$\frac{{m}^{2}kt}{{n}^{2}+{m}^{2}{k}^{2}}$=-$\frac{{m}^{2}k}{t}$,x0为切点的横坐标,
切点的纵坐标y0=kx0+t=$\frac{{n}^{2}}{t}$,
所以$\frac{{x}_{0}}{{y}_{0}}$=-$\frac{{m}^{2}k}{{n}^{2}}$,所以k=-$\frac{{n}^{2}{x}_{0}}{{m}^{2}{y}_{0}}$,
所以切线方程为:y-y0=k(x-x0)
=-$\frac{{n}^{2}{x}_{0}}{{m}^{2}{y}_{0}}$(x-x0),
化简得:$\frac{{x}_{0}x}{{m}^{2}}$+$\frac{{y}_{0}y}{{n}^{2}}$=1.
当切线斜率不存在时,切线为x=±m,也符合方程$\frac{{x}_{0}x}{{m}^{2}}$+$\frac{{y}_{0}y}{{n}^{2}}$=1,
综上$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)上一点Q(x0,y0)的切线方程为$\frac{{x}_{0}x}{{m}^{2}}$+$\frac{{y}_{0}y}{{n}^{2}}$=1;
(Ⅲ)设点P(xP,yP)为圆x2+y2=16上一点,
PA,PB是椭圆$\frac{{x}^{2}}{4}$+y2=1的切线,
切点A(x1,y1),B(x2,y2),过点A的椭圆的切线为$\frac{{x}_{1}x}{4}$+y1y=1,
过点B的椭圆的切线为$\frac{{x}_{2}x}{4}$+y2y=1.
由两切线都过P点,$\frac{{x}_{1}{x}_{P}}{4}$+y1yP=1,$\frac{{x}_{2}{x}_{P}}{4}$+y2yP=1
即有切点弦AB所在直线方程为$\frac{x{x}_{P}}{4}$+yyP=1.
M(0,$\frac{1}{{y}_{P}}$),N($\frac{4}{{x}_{P}}$,0),
|MN|2=$\frac{16}{{{x}_{P}}^{2}}$+$\frac{1}{{{y}_{P}}^{2}}$=($\frac{16}{{{x}_{P}}^{2}}$+$\frac{1}{{{y}_{P}}^{2}}$)•$\frac{{{x}_{P}}^{2}+{{y}_{P}}^{2}}{16}$
=$\frac{1}{16}$(17+$\frac{{{x}_{P}}^{2}}{{{y}_{P}}^{2}}$+$\frac{16{{y}_{P}}^{2}}{{{x}_{P}}^{2}}$)≥$\frac{1}{16}$(17+2$\sqrt{16}$)=$\frac{25}{16}$,
当且仅当$\frac{{{x}_{P}}^{2}}{{{y}_{P}}^{2}}$=$\frac{16{{y}_{P}}^{2}}{{{x}_{P}}^{2}}$即xP2=$\frac{64}{5}$,yP2=$\frac{16}{5}$时取等,
则|MN|$≥\frac{5}{4}$,即|MN|的最小值为$\frac{5}{4}$.
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率和方程的运用,考查直线和椭圆的位置关系,联立直线和椭圆方程,运用判别式为0,考查化简整理的运算能力,以及基本不等式的运用,属于中档题.

 名校课堂系列答案
名校课堂系列答案 如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.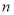 的值是( )
的值是( )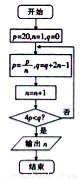
 ,若
,若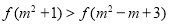 ,则实数
,则实数 的取值范围是( )
的取值范围是( ) B.
B.
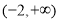 D.
D.
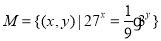 ,则下列说法正确的是( )
,则下列说法正确的是( )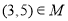 B.
B.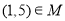
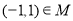 D.
D.