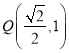题目内容
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,且对任意正整数n,点(
,且对任意正整数n,点(![]() ,
,![]() )在直线
)在直线![]() 上.
上.
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在实数λ,使得数列{![]() }为等差数列?若存在,求出λ的值;若不存在,请说明理由;
}为等差数列?若存在,求出λ的值;若不存在,请说明理由;
【答案】(1)an=(![]() )n-1;(2)λ=2.
)n-1;(2)λ=2.
【解析】试题分析:(Ⅰ)利用数列{an}的前n项Sn与an的关系得到数列相邻项之间的关系式,![]() 为等比数列,进而确定出其通项公式;
为等比数列,进而确定出其通项公式;
(Ⅱ)确定出数列{an}的前n项和为Sn的表达式是解决本题的关键,数列为等差数列首先保证其前3项满足等差数列的关系,得出关于λ的方程,从而确定出λ的值.
试题解析:
(1)由2an+1+Sn-2=0①
当n≥2时2an+Sn-1-2=0② ∴2an+1-2an+an=0 ∴![]() =
=![]() (n≥2)
(n≥2)
∵a1=1,2a2+a1=2a2=![]() ∴{an}是首项为1,公比为
∴{an}是首项为1,公比为![]() 的等比数列,
的等比数列,
∴an=(![]() )n-1.
)n-1.
(2)Sn=2-![]()
若![]() 为等差数列,则S1+λ+
为等差数列,则S1+λ+![]() ,S2+2λ+
,S2+2λ+![]() ,S3+3λ+
,S3+3λ+![]() 成等差数列,∴2(S2+2λ+
成等差数列,∴2(S2+2λ+![]() )=S1+
)=S1+![]() λ+S3+
λ+S3+![]() ∴λ=2,经检验知
∴λ=2,经检验知![]() 为等差数列。
为等差数列。

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目