Question

【题目】已知抛物线的焦点在直线上，且抛物线截直线所得的弦的长为．

（Ⅰ）求抛物线的方程和的值．

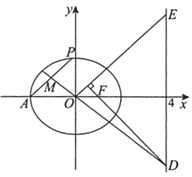
（Ⅱ）以弦为底边，以轴上点为顶点的三角形面积为，求点坐标．

Answer 1

【答案】（1）， （2）或

【解析】试题分析：（1）先求出抛物线焦点，确定抛物线方程，再与直线方程联立方程组，利用韦达定理及弦长公式求的值．（2）先设P点坐标，根据点到直线距离公式得P点到直线距离，即为高，再根据三角形面积公式列方程解出P点坐标，

试题解析：（Ⅰ）易知与轴的交点就是抛物线的焦点，

令，可得，

∴抛物线的焦点坐标为， ， ．

∴抛物线方程为．

联立方程组，

可得，

设交点为， ，

∴， ；

．

即： ，

解得．

（Ⅱ）∵， ，

∴到直线的距离为，

直线的方程为，设坐标为，

则有，

∴解得或，

∴坐标为或．