题目内容
【题目】平面直角坐标系中,动圆![]() 与圆
与圆![]() 外切,且与直线
外切,且与直线![]() 相切,记圆心
相切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设过定点![]() (
(![]() 为非零常数)的动直线
为非零常数)的动直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,问:在曲线
两点,问:在曲线![]() 上是否存在点
上是否存在点![]() (与
(与![]() 两点相异),当直线
两点相异),当直线![]() 的斜率存在时,直线
的斜率存在时,直线![]() 的斜率之和为定值.若存在,求出点
的斜率之和为定值.若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】【试题分析】(1)依据题设条件运用两圆位置关系建立方程求解;(2)依据题设条件借助直线的斜率公式及直线与抛物线的位置关系进行分析求解:
(1)不妨设动圆![]() 的圆心为
的圆心为![]() ,
,
易知圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,
,
∵动圆![]() 与圆
与圆![]() 外切,且与直线
外切,且与直线![]() 相切,
相切,
∴圆心![]() 在直线
在直线![]() 的右侧,且点
的右侧,且点![]() 到点
到点![]() 的距离比点
的距离比点![]() 到直线
到直线![]() 的距离大
的距离大![]() ,
,
即![]() ,且
,且![]() ,
,
∴![]() ,两边平方并化简整理得
,两边平方并化简整理得![]() ,
,
即曲线![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)假设在曲线![]() 上存在点
上存在点![]() 满足题设条件,不妨设
满足题设条件,不妨设![]() ,
,
则![]() ,
,
∴![]() (*)
(*)
显然动直线![]() 的斜率非零,故可设其方程为
的斜率非零,故可设其方程为![]() ,
,
联立![]() ,整理得
,整理得![]() ,
,
∴![]() ,且
,且![]() ,
,
代入(*)式得![]() ,
,
显然![]() ,于是
,于是![]() (**),
(**),
欲使(**)式对任意![]() 成立,∴
成立,∴ ,
,
显然![]() ,否则由
,否则由![]() 可知
可知![]() ,
,
从而可得![]() ,这与
,这与![]() 为非零常数矛盾,
为非零常数矛盾,
∴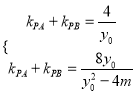 ,
,
∴![]() ,∴
,∴![]() ,
,
于是,当![]() 时,不存在满足条件的
时,不存在满足条件的![]() ,即不存在满足题设条件的点
,即不存在满足题设条件的点![]() ;
;
当![]() 时,
时, ![]() ,
,
将此代入抛物线![]() 的方程可求得满足条件的
的方程可求得满足条件的![]() 点坐标为
点坐标为![]() 或
或![]() .
.
下面说明此时直线![]() 的斜率必定存在,
的斜率必定存在,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
显然![]() ,∴
,∴![]() ,且
,且![]() ,∴直线
,∴直线![]() 的斜率必定存在,
的斜率必定存在,
综上所述,存在点![]() (与
(与![]() 两点相异),其坐标为
两点相异),其坐标为![]() ,或
,或![]() ,使得直线
,使得直线![]() 的斜率之和为定值.
的斜率之和为定值.

练习册系列答案
相关题目