题目内容
【题目】已知椭圆![]() :
: ![]() ,过点
,过点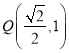 作圆
作圆![]() 的切线,切点分别为
的切线,切点分别为![]() ,
, ![]() ,直线
,直线![]() 恰好经过椭圆
恰好经过椭圆![]() 的右顶点和上顶点.
的右顶点和上顶点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
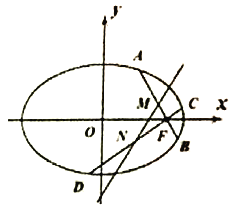
(Ⅱ)如图,过椭圆![]() 的右焦点
的右焦点![]() 作两条互相垂直的弦
作两条互相垂直的弦![]() ,
, ![]() ,设
,设![]() ,
, ![]() 的中点分别为
的中点分别为![]() ,
, ![]() ,证明:直线
,证明:直线![]() 必过定点,并求此定点坐标.
必过定点,并求此定点坐标.
【答案】(1)![]() (2)直线
(2)直线![]() 过点
过点![]() .
.
【解析】试题分析:(1)先根据直线与圆相切求切线方程,再根据椭圆几何条件确定![]() ,
, ![]() ,(2)直线过定点问题,一般先利用特殊情况确定定点,转化为证三点共线:先联立直线
,(2)直线过定点问题,一般先利用特殊情况确定定点,转化为证三点共线:先联立直线![]() :
: ![]() ,与椭圆方程,利用韦达定理及中点坐标公式求
,与椭圆方程,利用韦达定理及中点坐标公式求![]() 中点
中点![]() (用直线AB斜率表示),同理可得
(用直线AB斜率表示),同理可得![]() 点坐标,利用两点斜率公式证三点共线.
点坐标,利用两点斜率公式证三点共线.
试题解析:(Ⅰ)由切点弦方程知切线方程为![]() ,令
,令![]() ,则
,则![]() ,所以上顶点的坐标为
,所以上顶点的坐标为![]() ,
,
所以![]() ,令
,令![]() ,则
,则![]() ,
,
所以右顶点的坐标为![]() ,所以
,所以![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)若直线![]() ,
, ![]() 斜率均存在,设直线
斜率均存在,设直线![]() :
: ![]() ,
, ![]() ,
, ![]() ,
,
则中点![]() .先考虑
.先考虑![]() 的情形.
的情形.
由![]() 得
得![]() ,
,
由直线![]() 过点
过点![]() ,可知判别式
,可知判别式![]() 恒成立,
恒成立,
由韦达定理,得![]() ,故
,故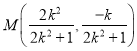 ,同理可得
,同理可得![]() .
.
若![]() ,得
,得![]() ,则直线
,则直线![]() 斜率不存在,此时直线
斜率不存在,此时直线![]() 过点
过点![]() .
.
另当![]() 斜率为0时,直线
斜率为0时,直线![]() 也过点
也过点![]() .
.
下证动直线![]() 过定点
过定点![]() ,
,
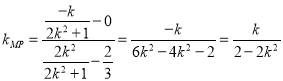 ,
,  ,
,
∴![]() ,即直线
,即直线![]() 过点
过点![]() .
.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目