题目内容
【题目】抛物线![]() :
:![]() 过点
过点![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设![]() 为
为![]() 轴上一点,
轴上一点,![]() 为抛物线上任意一点,求
为抛物线上任意一点,求![]() 的最小值;
的最小值;
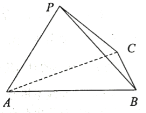
(3)过抛物线![]() 的焦点
的焦点![]() ,作相互垂直的两条弦
,作相互垂直的两条弦![]() 和
和![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)当
(2)当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;当
;当![]() 时,
时,![]() 的最小值为
的最小值为![]() (3)32
(3)32
【解析】
(1)将点![]() 代入抛物线方程,解出
代入抛物线方程,解出![]() ,即可求出;
,即可求出;
(2)设出点![]() ,根据距离公式表示出
,根据距离公式表示出![]() ,再根据二次函数知识即可求出;
,再根据二次函数知识即可求出;
(3)由题可知两直线斜率都存在,所以设![]() :
:![]() ,
,![]() :
:![]() ,将直线方程与抛物线方程联立,利用韦达定理求出
,将直线方程与抛物线方程联立,利用韦达定理求出![]() ,
,![]() ,根据弦长公式即可求出
,根据弦长公式即可求出![]() 和
和![]() 的长,然后根据基本不等式即可求出.
的长,然后根据基本不等式即可求出.
(1)将点![]() 代入抛物线方程,得
代入抛物线方程,得![]() ,解得
,解得![]() ,
,
所以抛物线![]() 的方程为:
的方程为:![]() .
.
(2)设点![]() ,则
,则![]() ,
,![]() .
.
所以![]() .
.
设![]() ,对称轴为
,对称轴为![]() ,
,
当![]() 即
即![]() 时,
时,![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,即
,即![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以
上单调递增,所以![]() ,
,![]() 的最小值为
的最小值为![]() .
.
综上,当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;当
;当![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
(3)由题可知两直线斜率都存在,设![]() ,
,![]() ,
,
![]() :
:![]() ,
,![]() :
:![]() ,
,
由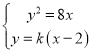 ,化简得,
,化简得,![]() ,所以
,所以![]() ,
,
同理可得,![]() ,即
,即![]() ,
,![]() ,
,
故![]() .
.
即![]() 的最小值为32.
的最小值为32.

【题目】某大城市一家餐饮企业为了了解外卖情况,统计了某个送外卖小哥某天从9:00到21:00这个时间段送的50单外卖.以2小时为一时间段将时间分成六段,各时间段内外卖小哥平均每单的收入情况如下表,各时间段内送外卖的单数的频率分布直方图如下图.
时间区间 |
|
|
|
|
|
|
每单收入(元) | 6 | 5.5 | 6 | 6.4 | 5.5 | 6.5 |
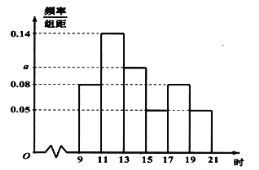
(Ⅰ)求频率分布直方图中![]() 的值,并求这个外卖小哥送这50单获得的收入;
的值,并求这个外卖小哥送这50单获得的收入;
(Ⅱ)在这个外卖小哥送出的50单外卖中男性订了25单,且男性订的外卖中有20单带饮品,女性订的外卖中有10单带饮品,请完成下面的![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“带饮品和男女性别有关”?
的把握认为“带饮品和男女性别有关”?
带饮品 | 不带饮品 | 总计 | |
男 | |||
女 | |||
总计 |
附:![]()
| 0.050 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
【题目】某中学为研究学生的身体素质与体育锻炼时间的关系,对该校200名高三学生平均每天体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
平均每天锻炼的时间/分钟 |
|
|
|
|
|
|
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
将学生日均体育锻炼时间在![]() 的学生评价为“锻炼达标”.
的学生评价为“锻炼达标”.
(1)请根据上述表格中的统计数据填写下面的![]() 列联表;
列联表;
锻炼不达标 | 锻炼达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
并通过计算判断,是否能在犯错误的概率不超过0.025的前提下认为“锻炼达标”与性别有关?
(2)在“锻炼达标”的学生中,按男女用分层抽样方法抽出5人,进行体育锻炼体会交流,再从这5人中选出2人作重点发言,求作重点发言的2人中,至少1人是女生的概率.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |