题目内容

【题目】在直角坐标系中，曲线的参数方程为（为参数）.以坐标原点为极点，轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为.

（1）求曲线的极坐标方程和曲线的参数方程；

（2）若曲线与曲线，在第一象限分别交于两点，且，求的取值范围.

【答案】（1）见解析（2）.

【解析】

(1)根据极坐标化为直角坐标的公式得到相应的极坐标方程，根据直角坐标和参数方程的互化得到参数方程；（2）联立极坐标方程得到，同理得到，所以 ，进而得到结果.

（1）依题意，得曲线的直角坐标方程为.

由得曲线的极坐标方程为，即为.

由曲线的极坐标方程，得，

所以曲线的直角坐标方程为，即.

所以曲线的参数方程为（为参数）.

（2）设曲线.因为，所以.

联立，得.

联立得.

所以 ，

即的取值范围为.

练习册系列答案
相关题目

【题目】如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，AB=2AD=2，∠DAB=60°，PA=PC=2，且平面ACP⊥平面ABCD．

（Ⅰ）求证：CB⊥PD；

（Ⅱ）求二面角C-PB-A的余弦值．

【题目】定义：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”．如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比．已知椭圆．

（1）若椭圆，判断与是否相似？如果相似，求出与的相似比；如果不相似，请说明理由；

（2）写出与椭圆相似且短半轴长为的椭圆的方程；若在椭圆上存在两点、关于直线对称，求实数的取值范围．

【题目】已知函数.

（1）当时，求函数的极值；

（2）证明：当时，.

【题目】关于的方程组的系数矩阵记为，且该方程组存在非零解，若存在三阶矩阵，使得，（0表示零矩阵，即所有元素均为0的矩阵；矩阵对应的行列式为），则

（1）一定为1；

（2）一定为0；

（3）该方程组一定有无穷多解.

其中正确说法的个数是（ ）

A.0B.1C.2D.3

【题目】新个税法于2019年1月1日进行实施.为了调查国企员工对新个税法的满意程度，研究人员在地各个国企中随机抽取了1000名员工进行调查，并将满意程度以分数的形式统计成如下的频率分布直方图，其中.

（Ⅰ）估计被调查的员工的满意程度的中位数；（计算结果保留两位小数）

（Ⅱ）若按照分层抽样从，中随机抽取8人，再从这8人中随机抽取4人，记分数在的人数为，求的分布列与数学期望；

（Ⅲ）以频率估计概率，若该研究人员从全国国企员工中随机抽取人作调查，记成绩在，的人数为，若，求的最大值.

【题目】在直角坐标系中，曲线的参数方程为（为参数）.以坐标原点为极点，轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为.

（1）求曲线的极坐标方程和曲线的参数方程；

（2）若曲线与曲线，在第一象限分别交于两点，且，求的取值范围.

【题目】某大城市一家餐饮企业为了了解外卖情况，统计了某个送外卖小哥某天从9:00到21:00这个时间段送的50单外卖.以2小时为一时间段将时间分成六段，各时间段内外卖小哥平均每单的收入情况如下表，各时间段内送外卖的单数的频率分布直方图如下图.

时间区间

每单收入（元）

6

5.5

6

6.4

5.5

6.5

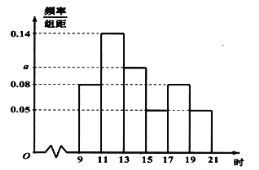
（Ⅰ）求频率分布直方图中的值，并求这个外卖小哥送这50单获得的收入；

（Ⅱ）在这个外卖小哥送出的50单外卖中男性订了25单，且男性订的外卖中有20单带饮品，女性订的外卖中有10单带饮品，请完成下面的列联表，并回答是否有的把握认为“带饮品和男女性别有关”？

带饮品

不带饮品

总计

男

女

总计

附：

0.050

0.010

0.005

0.001

3.841

6.635

7.879

10.828

【题目】记无穷数列的前项中最大值为，最小值为，令．

（1）若，写出，，，的值；

（2）设，若，求的值及时数列的前项和；

（3）求证：“数列是等差数列”的充要条件是“数列是等差数列”．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网