题目内容
在正三角形ABC的边AB、AC上分别取D、E两点,使沿线段DE折叠三角形时,顶点A正好落在边BC上,在这种情况下,若要使AD最小,求AD∶AB的值.
AD∶DB=2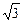 -3
-3
 -3
-3 按题意,设折叠后A点落在边BC上改称P点,显然A、P两点关于折线DE对称,又设∠BAP=θ,∴∠DPA=θ,∠BDP=2θ,
再设AB=a,AD=x,∴DP=x 在△ABC中,
在△ABC中,
∠APB=180°-∠ABP-∠BAP=120°-θ,
由正弦定理知: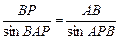
 ∴BP=
∴BP=
在△PBD中,
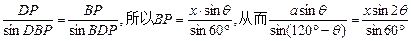 ,
,
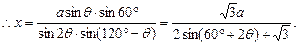
∵0°≤θ≤60°,∴60°≤60°+2θ≤180°,
∴当60°+2θ=90°,即θ=15°时,
sin(60°+2θ)=1,此时x取得最小值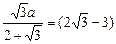 a,即AD最小,
a,即AD最小,
∴AD∶DB=2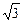 -3.
-3.
再设AB=a,AD=x,∴DP=x
 在△ABC中,
在△ABC中,∠APB=180°-∠ABP-∠BAP=120°-θ,
由正弦定理知:
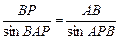
 ∴BP=
∴BP=
在△PBD中,
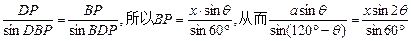 ,
,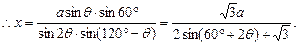
∵0°≤θ≤60°,∴60°≤60°+2θ≤180°,
∴当60°+2θ=90°,即θ=15°时,
sin(60°+2θ)=1,此时x取得最小值
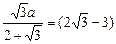 a,即AD最小,
a,即AD最小,∴AD∶DB=2
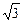 -3.
-3.
练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
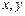 为正实数,
为正实数,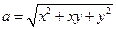 ,
,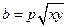 ,
,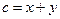 。
。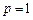 ,则是否存在以
,则是否存在以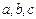 为三边长的三角形?请说明理由;
为三边长的三角形?请说明理由;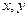 ,试探索当存在以
,试探索当存在以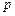 的取值范围。
的取值范围。 中,角
中,角 、
、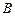 、
、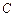 的对边分别为
的对边分别为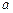 、
、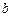 、
、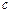 ,若
,若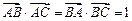 .
.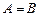 ;⑵求边长
;⑵求边长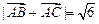 ,求△
,求△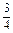 .
.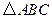 中,
中,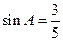 ,
,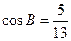 ,求
,求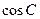 的值.
的值.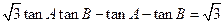 .(I)求∠C的大小;(Ⅱ)设角A,B,C的对边依次为
.(I)求∠C的大小;(Ⅱ)设角A,B,C的对边依次为 ,若
,若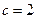 ,且△ABC是锐角三角形,求
,且△ABC是锐角三角形,求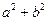 的取值范围.
的取值范围. 的圆,且
的圆,且
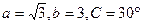 ,则A= 。
,则A= 。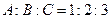 ,则
,则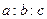 等于( )
等于( )