题目内容
设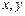 为正实数,
为正实数,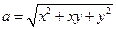 ,
,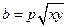 ,
,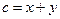 。
。
(Ⅰ)如果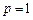 ,则是否存在以
,则是否存在以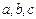 为三边长的三角形?请说明理由;
为三边长的三角形?请说明理由;
(Ⅱ)对任意的正实数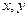 ,试探索当存在以
,试探索当存在以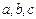 为三边长的三角形时
为三边长的三角形时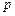 的取值范围。
的取值范围。
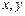 为正实数,
为正实数,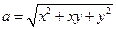 ,
,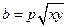 ,
,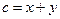 。
。(Ⅰ)如果
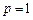 ,则是否存在以
,则是否存在以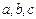 为三边长的三角形?请说明理由;
为三边长的三角形?请说明理由;(Ⅱ)对任意的正实数
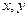 ,试探索当存在以
,试探索当存在以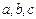 为三边长的三角形时
为三边长的三角形时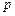 的取值范围。
的取值范围。(Ⅰ)存在,理由见解析。
(Ⅱ)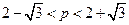
(Ⅱ)
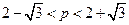
(Ⅰ)存在.……2分
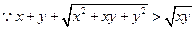 显然成立,
显然成立,
且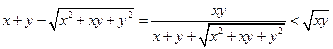 ,
,
由于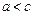 ,所以我们得到
,所以我们得到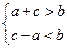 ,
,
即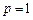 时,存在以
时,存在以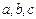 为三边长的三角形。……6分
为三边长的三角形。……6分
(Ⅱ)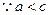 ,
,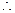 若
若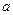 、
、 、
、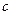 构成三角形,只需
构成三角形,只需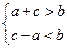 ,
,
即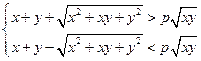 ……8分
……8分
两边除以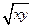 ,令
,令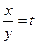 ,得
,得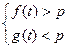 ,这里
,这里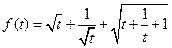 ,
,
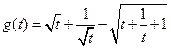 ,……12分
,……12分
由于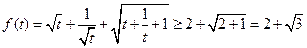 ,
,
所以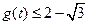 ,当且仅当
,当且仅当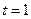 时,
时,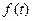 取最小值
取最小值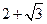 ,
,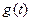 取最大值
取最大值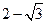 ;
;
因此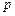 的取值范围为
的取值范围为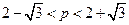 ,
,
即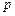 的取值范围为
的取值范围为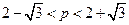 时,
时,
以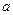 、
、 、
、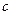 为三边的三角形总存在。……15分
为三边的三角形总存在。……15分
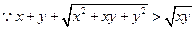 显然成立,
显然成立,且
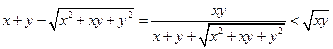 ,
,由于
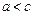 ,所以我们得到
,所以我们得到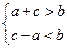 ,
,即
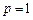 时,存在以
时,存在以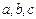 为三边长的三角形。……6分
为三边长的三角形。……6分(Ⅱ)
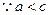 ,
,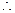 若
若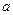 、
、 、
、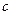 构成三角形,只需
构成三角形,只需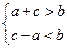 ,
,即
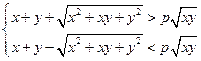 ……8分
……8分两边除以
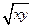 ,令
,令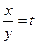 ,得
,得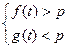 ,这里
,这里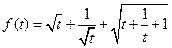 ,
,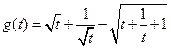 ,……12分
,……12分由于
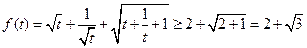 ,
,所以
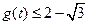 ,当且仅当
,当且仅当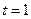 时,
时,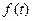 取最小值
取最小值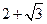 ,
,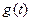 取最大值
取最大值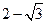 ;
;因此
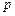 的取值范围为
的取值范围为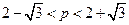 ,
,即
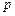 的取值范围为
的取值范围为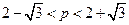 时,
时,以
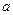 、
、 、
、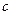 为三边的三角形总存在。……15分
为三边的三角形总存在。……15分
练习册系列答案
相关题目
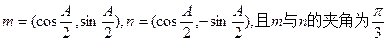 。
。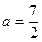 ,求bc的最大值。
,求bc的最大值。 ,且
,且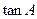 与
与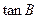 是方程
是方程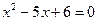 的两个根.
的两个根.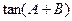 的值;
的值; ,求BC的长.
,求BC的长.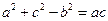 .(Ⅰ)求角
.(Ⅰ)求角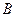 的大小;(Ⅱ)若
的大小;(Ⅱ)若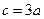 ,求
,求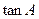 的值.
的值.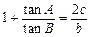 .
.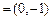 ,n
,n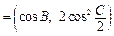 ,试求|m
,试求|m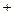 n|的最小值。
n|的最小值。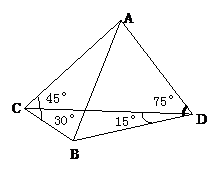



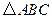 中,
中,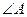 最大,
最大,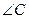 最小,且
最小,且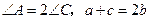 ,求此三角形三边之比.
,求此三角形三边之比.