题目内容
已知函数f(x)＝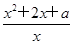
，x∈[1，＋∞)．
(1)当a＝4时，求函数f(x)的最小值；
(2)若对任意x∈[1，＋∞)，f(x)>0恒成立，试求实数a的取值范围．
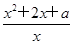，x∈[1，＋∞)．(1)当a＝4时，求函数f(x)的最小值；
(2)若对任意x∈[1，＋∞)，f(x)>0恒成立，试求实数a的取值范围．
（1）6（2）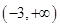
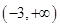
(1)由a＝4，∴f(x)＝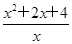
＝x＋
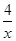＋2≥6，当x＝2时，取得等号．即当x＝2时，f(x)min＝6.
(2)x∈[1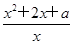，＋∞)， >0恒成立，即x∈[1，＋∞)，x2＋2x＋a>0恒成立．
等价于a>－x2－2x，当x∈[1，＋∞)时恒成立，
令g(x)＝－x2－2x，x∈[1，＋∞)，
∴a>g(x)max＝－1－2×1＝－3，即a>－3.∴a的取值范围是.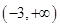
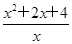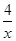＝x＋＋2≥6，当x＝2时，取得等号．即当x＝2时，f(x)min＝6.(2)x∈[1，＋∞)，
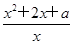>0恒成立，即x∈[1，＋∞)，x2＋2x＋a>0恒成立．等价于a>－x2－2x，当x∈[1，＋∞)时恒成立，
令g(x)＝－x2－2x，x∈[1，＋∞)，
∴a>g(x)max＝－1－2×1＝－3，即a>－3.∴a的取值范围是
.
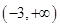练习册系列答案
相关题目
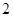万元购进一台新设备用于生产. 第一年需运营费用
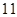万元. 设该设备使用了
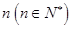年后，年平均盈利额达到最大值（盈利额等于收入减去成本），则
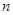等于（）
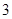
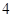
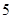
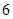
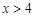，则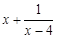
的最小值_________.
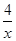的最小值为________．
+
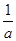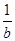的最小值为( )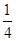
+
＋
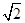
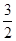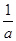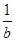的最小值是________．
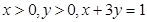，则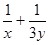
的最小值为_____ 。