题目内容
设函数f(x)=
,若f(-4)=f(0),f(-2)=-2,则函数g(x)=f(x)-x的零点个数为______.
|
由f(-4)=f(0)得16-4b+c=c,解得b=4.又f(-2)=-2,即4-8+c=-2,解得c=2.
所以f(x)=
,由g(x)=0,得f(x)=x,在同一个坐标系中,分别作出函数y=f(x),y=x图象,
如图:由图象可知两图象有三个交点,所以函数g(x)=f(x)-x的零点个数为3个.
故答案为:3
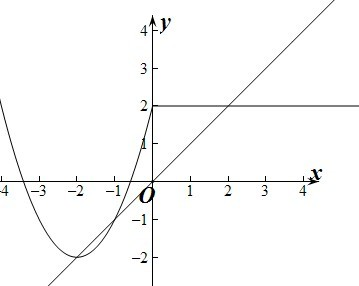
所以f(x)=
|
如图:由图象可知两图象有三个交点,所以函数g(x)=f(x)-x的零点个数为3个.
故答案为:3
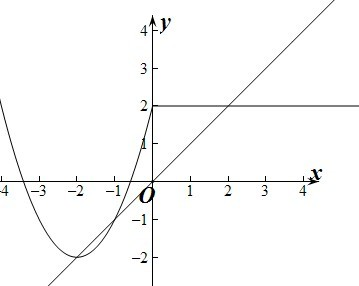

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的一个零点在
的一个零点在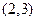 内,则实数
内,则实数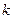 的取值范围是( )
的取值范围是( )