题目内容
已知函数函f(x)=x|x|-2x(x∈R)
(1)判断函数的奇偶性,并用定义证明;
(2)作出函数f(x)=x|x|-2x的图象;
(3)讨论方程x|x|-2x=a根的情况.

(1)判断函数的奇偶性,并用定义证明;
(2)作出函数f(x)=x|x|-2x的图象;
(3)讨论方程x|x|-2x=a根的情况.

(1)∵f(x)=x|x|-2x=
∴当x>0时,-x<0,故f(-x)=-x2+2x,=-f(x)
当x<0时,-x>0,故f(-x)=x2+2x=-f(x)
当x=0时,-x=0,故f(-x)=-f(x)=0
综上函数f(x)=x|x|-2x为奇函数
(2)由(1)中f(x)=x|x|-2x=
则函数的图象如下图所示:
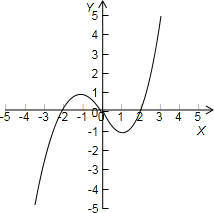
(3)由图可知:
当a<-1,或a>1时,方程x|x|-2x=a有一个根;
当a=-1,或a=1时,方程x|x|-2x=a有二个根;
当-1<a<1时,方程x|x|-2x=a有三个根;
|
∴当x>0时,-x<0,故f(-x)=-x2+2x,=-f(x)
当x<0时,-x>0,故f(-x)=x2+2x=-f(x)
当x=0时,-x=0,故f(-x)=-f(x)=0
综上函数f(x)=x|x|-2x为奇函数
(2)由(1)中f(x)=x|x|-2x=
|
则函数的图象如下图所示:
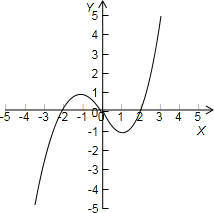
(3)由图可知:
当a<-1,或a>1时,方程x|x|-2x=a有一个根;
当a=-1,或a=1时,方程x|x|-2x=a有二个根;
当-1<a<1时,方程x|x|-2x=a有三个根;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



