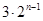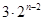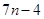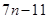题目内容
已知数列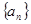 中,
中,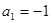 ,
,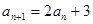 .
.
(1)若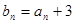 ,证明
,证明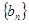 是等比数列;
是等比数列;
(2)求数列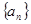 的通项公式;
的通项公式;
(3)若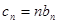 ,求数列
,求数列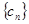 的前
的前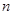 项和
项和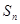 .
.
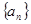 中,
中,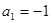 ,
,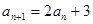 .
.(1)若
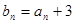 ,证明
,证明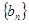 是等比数列;
是等比数列;(2)求数列
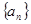 的通项公式;
的通项公式;(3)若
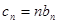 ,求数列
,求数列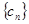 的前
的前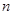 项和
项和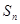 .
.(1) 见解析(2)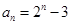 (3)
(3)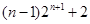
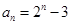 (3)
(3)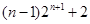
本试题主要是考查了数列的定义和数列的通项公式的求解以及数列求和的综合运用。
(1)由题意得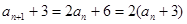
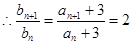
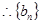 是首项为
是首项为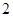 ,公比为
,公比为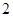 的等比数列。
的等比数列。
(2)因为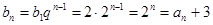
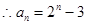
(3)因为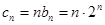
,那么利用错位相减法可知和式。
解:(1)由题意得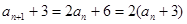
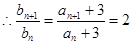
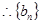 是首项为
是首项为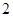 ,公比为
,公比为 的等比数列。
的等比数列。
(2)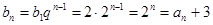
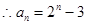
(3)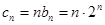
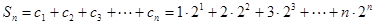 ……①
……①
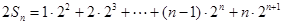 ……②
……②
①-②得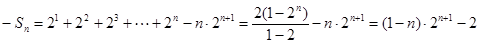
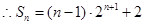
(1)由题意得
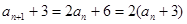
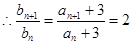
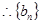 是首项为
是首项为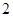 ,公比为
,公比为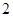 的等比数列。
的等比数列。(2)因为
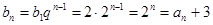
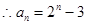
(3)因为
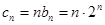
,那么利用错位相减法可知和式。
解:(1)由题意得
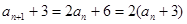
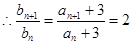
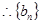 是首项为
是首项为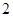 ,公比为
,公比为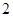 的等比数列。
的等比数列。(2)
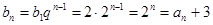
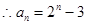
(3)
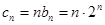
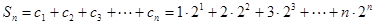 ……①
……①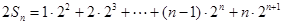 ……②
……②①-②得
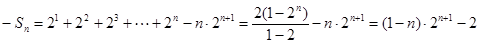
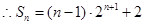

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
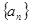 的前
的前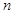 项和
项和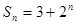 ,则数列
,则数列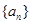 的前
的前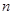 项和为
项和为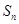 ,且有
,且有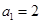 ,
,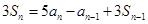
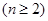
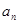 的通项公式;
的通项公式;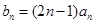 ,求数列
,求数列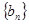 的前
的前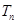 。山大附中
。山大附中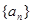 是等差数列,则当
是等差数列,则当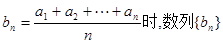 也是等差数列;类比上述性质,相应地
也是等差数列;类比上述性质,相应地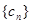 是正项等比数列,当
是正项等比数列,当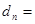 时,数列
时,数列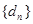 也是等比数列。
也是等比数列。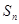 是等差数列
是等差数列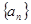 的前
的前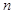 项和,
项和,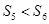 ,
,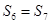 ,
,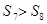 则下列结论中错误的( )
则下列结论中错误的( )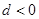
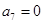
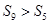
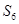 与
与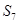 均为
均为 ,
,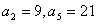
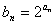 ,求数列
,求数列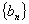 的前
的前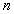 项和
项和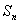 ;
;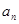 }是等差数列,
}是等差数列,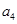 =7,则
=7,则 =_________
=_________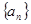 中,
中,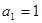 ,
,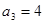 ,则公差
,则公差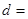 ( )
( )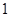
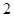

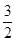
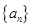 中,若
中,若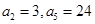 ,则通项
,则通项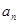 = ( )
= ( )