题目内容
(满分12分)3.已知数列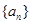 的前
的前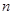 项和为
项和为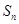 ,且有
,且有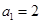 ,
,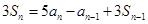
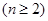
(1)求数列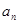 的通项公式;
的通项公式;
(2)若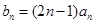 ,求数列
,求数列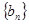 的前
的前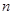 项的和
项的和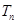 。山大附中
。山大附中
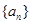 的前
的前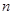 项和为
项和为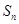 ,且有
,且有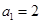 ,
,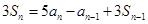
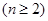
(1)求数列
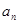 的通项公式;
的通项公式;(2)若
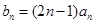 ,求数列
,求数列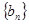 的前
的前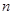 项的和
项的和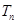 。山大附中
。山大附中(1)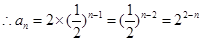 ;(2)
;(2)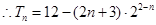 。
。
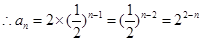 ;(2)
;(2)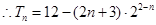 。
。本试题主要是考查了数列的前n项和与通项公式的关系的转化和求解的运用,以及运用错位相减法求解数列和的重要数学思想的运用。
(1)由于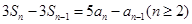 ,因此可知
,因此可知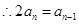 ,从而得到通项公式。
,从而得到通项公式。
(2)由1可知,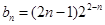 ,那么利用错位相减法得到数列的和的运用。
,那么利用错位相减法得到数列的和的运用。
解:(1)由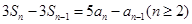 ,
,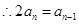 ……2分
……2分
又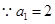 ,
,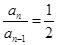
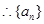 是以2为首项,
是以2为首项,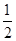 为公比的等比数列,……4分
为公比的等比数列,……4分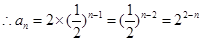 ……5分
……5分
(2)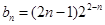
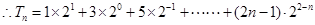 (1)
(1)
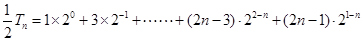 (2)……8分
(2)……8分
(1)—(2)得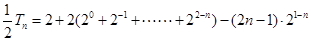 ……10分
……10分
即: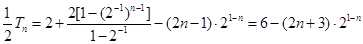 ,
, 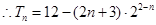 ……12分
……12分
(1)由于
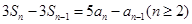 ,因此可知
,因此可知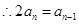 ,从而得到通项公式。
,从而得到通项公式。(2)由1可知,
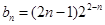 ,那么利用错位相减法得到数列的和的运用。
,那么利用错位相减法得到数列的和的运用。解:(1)由
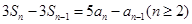 ,
,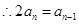 ……2分
……2分又
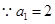 ,
,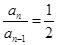
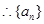 是以2为首项,
是以2为首项,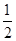 为公比的等比数列,……4分
为公比的等比数列,……4分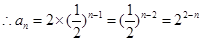 ……5分
……5分(2)
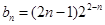
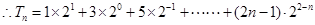 (1)
(1)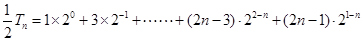 (2)……8分
(2)……8分(1)—(2)得
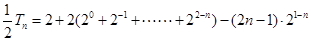 ……10分
……10分即:
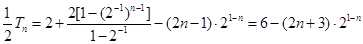 ,
, 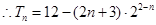 ……12分
……12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
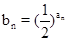 ,记数列{bn}的前n项和为Tn,
,记数列{bn}的前n项和为Tn,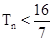 (n∈N*).
(n∈N*).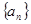 中,
中,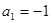 ,
,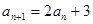 .
.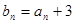 ,证明
,证明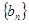 是等比数列;
是等比数列;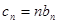 ,求数列
,求数列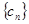 的前
的前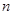 项和
项和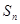 .
.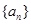 为等差数列,且
为等差数列,且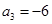 ,
,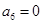 .
.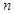 项和
项和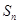 的最小值;
的最小值;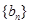 满足
满足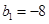 ,
,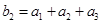 ,求
,求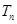 .
.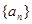 为等差数列,首项为
为等差数列,首项为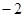 ,公差为5,则该数列的第8项为( )
,公差为5,则该数列的第8项为( )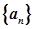 的前
的前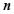 项和记为
项和记为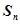 ,已知
,已知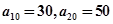 ;
;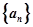 的通项
的通项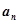
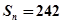 ,求
,求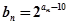 ,求数列
,求数列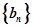 的前
的前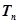
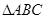 的三个角
的三个角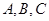 的对边分别为
的对边分别为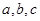 ,且
,且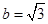 。数列
。数列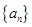 是等比数列,且首项
是等比数列,且首项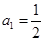 ,公比为
,公比为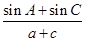 。
。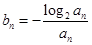 ,求数列
,求数列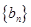 的前
的前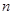 项和
项和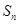 。
。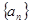 的前
的前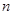 项和为
项和为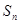 ,已知
,已知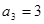 ,
,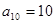 ,则
,则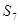 的值是
的值是