题目内容
8．
如图，已知AB⊥平面ACD，DE⊥平面ACD，三角形ACD是正三角形，且AD=DE=2AB，F是CD的中点．（1）求证：平面CBE⊥平面CDE；
（2）求二面角C-BE-F的余弦值．
分析 （1）取CE的中点M，连接BM、FM，通过证明BM⊥平面CDE，利用平面与平面垂直的判定定理证明平面 BCE⊥平面 CDE．
（2）过F作FN⊥CE交CE于N，过N作NH⊥BE，连接HF，则∠NHF就是二面角C-BE-F的平面角．
解答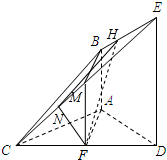 
（1）证明：因为DE⊥平面ACD，DE?平面CDE，
所以平面CDE⊥平面ACD．
在底面ACD中，AF⊥CD，由面面垂直的性质定理知，AF⊥平面CDE．
取CE的中点M，连接BM、FM，
由已知可得FM=AB且FM∥AB，则四边形FMBA为平行四边形，从而BM∥AF．
所以BM⊥平面CDE．
又BM?平面BCE，则平面CBE⊥平面CDE．…（7分）
（2）解：过F作FN⊥CE交CE于N，过N作NH⊥BE，连接HF，
则∠NHF就是二面角C-BE-F的平面角．
在Rt△FNH中，NH=$\frac{3\sqrt{6}}{2\sqrt{5}}$，FH=$\frac{4}{\sqrt{5}}$，
所以cos∠NHF=$\frac{NH}{FH}$=$\frac{3\sqrt{6}}{8}$
故二面角C-BE-F的余弦值为$\frac{3\sqrt{6}}{8}$…（15分）
点评 本题考查平面与平面垂直的判定，考查二面角的余弦值，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
18．三个实数a、b、c成等比数列，且a+b+c=6，则b的取值范围是（ ）
| A． | [-6，2] | B． | [-6，0）∪（ 0，2] | C． | [-2，0）∪（ 0，6] | D． | （0，2] |
16．已知命题p：sinα-cosα=$\sqrt{2}$，命题q：双曲线$\frac{{x}^{2}}{co{s}^{2}α}$-$\frac{{y}^{2}}{si{n}^{2}α}$=1的渐近线与圆x2+（y-1）2=$\frac{1}{2}$相切，则命题p为命题q为（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
3．在△ABC中，内角A，B，C的对边分别为a，b，c，若a=3，b=2$\sqrt{6}$，∠B=2∠A，则cosA的值为（ ）
| A． | $\frac{{\sqrt{6}}}{3}$ | B． | $\frac{{2\sqrt{6}}}{3}$ | C． | $\frac{{\sqrt{6}}}{6}$ | D． | $\frac{{\sqrt{6}}}{8}$ |
13．已知函数f（x）=|2x+1|+|2x-3|，若关于x的不等式f（x）＜|a-1|的解集非空，则实数a的取值范围是（ ）
| A． | [-3，5] | B． | （-3，5） | C． | （-∞，-3]∪[5，+∞） | D． | （-∞，-3）∪（5，+∞） |
20．已知底面边长为$\sqrt{3}$的正三棱柱ABC-A1B1C1的体积为$\frac{9}{4}$，若点P为底面A1B1C1的中心，则PA与平面ABC所成角的大小为（ ）
| A． | $\frac{5π}{12}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{6}$ |