题目内容
18.三个实数a、b、c成等比数列,且a+b+c=6,则b的取值范围是( )| A. | [-6,2] | B. | [-6,0)∪( 0,2] | C. | [-2,0)∪( 0,6] | D. | (0,2] |
分析 设此等比数列的公比为q,由a+b+c=6,可得$\frac{b}{q}+b+bq$=6,变形为b=$\frac{6}{\frac{1}{q}+q+1}$.对q分类讨论,再利用基本不等式的性质即可得出.
解答 解:设此等比数列的公比为q,
∵a+b+c=6,
∴$\frac{b}{q}+b+bq$=6,
∴b=$\frac{6}{\frac{1}{q}+q+1}$.
当q>0时,$b≤\frac{6}{2\sqrt{q•\frac{1}{q}}+1}$=2,当且仅当q=1时取等号,此时b∈(0,2];
当q<0时,b$≥\frac{6}{-2\sqrt{(-q)•\frac{1}{-q}}+1}$=-6,当且仅当q=-1时取等号,此时b∈[-6,0).
∴b的取值范围是[-6,0)∪( 0,2].
故选:B.
点评 本题考查了等比数列的通项公式、基本不等式的性质、分类讨论思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.已知D是△ABC所在平面内一点,$\overrightarrow{AD}$=$\frac{7}{13}$$\overrightarrow{AB}$+$\frac{6}{13}$$\overrightarrow{AC}$,则( )
| A. | $\overrightarrow{BD}$=$\frac{7}{13}$$\overrightarrow{BC}$ | B. | $\overrightarrow{BD}$=$\frac{6}{13}$$\overrightarrow{BC}$ | C. | $\overrightarrow{BD}$=$\frac{13}{7}$$\overrightarrow{BC}$ | D. | $\overrightarrow{BD}$=$\frac{13}{6}$$\overrightarrow{BC}$ |
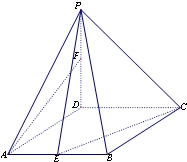 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.
 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.