题目内容
20.已知底面边长为$\sqrt{3}$的正三棱柱ABC-A1B1C1的体积为$\frac{9}{4}$,若点P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 利用三棱柱ABC-A1B1C1的侧棱与底面垂直和线面角的定义可知,∠APA1为PA与平面A1B1C1所成角,即为∠APA1为PA与平面ABC所成角.利用三棱锥的体积计算公式可得AA1,再利用正三角形的性质可得A1P,在Rt△AA1P中,利用tan∠APA1=$\frac{A{A}_{1}}{{A}_{1}P}$即可得出
解答 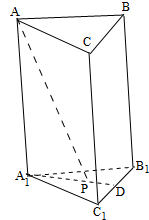 解:如图所示,
解:如图所示,
∵AA1⊥底面A1B1C1,∴∠APA1为PA与平面A1B1C1所成角,
∵平面ABC∥平面A1B1C1,∴∠APA1为PA与平面ABC所成角.
∵S△A1B1C1=$\frac{\sqrt{3}}{4}$×($\sqrt{3}$)2=$\frac{3\sqrt{3}}{4}$,.
∴${V}_{三棱柱ABC-{A}_{1}{B}_{1}{C}_{1}}$=AA1×S△A1B1C1=$\frac{3\sqrt{3}}{4}$×AA1=$\frac{9}{4}$,解得AA1=$\sqrt{3}$.
又P为底面正三角形A1B1C1的中心,
∴A1P=$\frac{2}{3}$×A1D=$\frac{2}{3}$×$\sqrt{3}×\frac{\sqrt{3}}{2}$=1,
在Rt△AA1P中,tan∠APA1=$\frac{A{A}_{1}}{{A}_{1}P}$=$\sqrt{3}$,
∠APA1=$\frac{π}{3}$.
故选:B
点评 熟练掌握三棱柱的性质、体积计算公式、正三角形的性质、线面角的定义是解题的关键,把空间角转化为平面角问题求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 将正方形ABCD分割成n2(n≥2,n∈N)个全等的小正方形(图1,图2分别给出了n=2,3的情形),在每个小正方形的顶点各放置一个数,使位于正方形ABCD的四边及平行于某边的任一直线上的数都分别依次成等差数列,若顶点A,B,C,D处的四个数互不相同且和为1,记所有顶点上的数之和为f(n),则f(4)=( )
将正方形ABCD分割成n2(n≥2,n∈N)个全等的小正方形(图1,图2分别给出了n=2,3的情形),在每个小正方形的顶点各放置一个数,使位于正方形ABCD的四边及平行于某边的任一直线上的数都分别依次成等差数列,若顶点A,B,C,D处的四个数互不相同且和为1,记所有顶点上的数之和为f(n),则f(4)=( )
 将正方形ABCD分割成n2(n≥2,n∈N)个全等的小正方形(图1,图2分别给出了n=2,3的情形),在每个小正方形的顶点各放置一个数,使位于正方形ABCD的四边及平行于某边的任一直线上的数都分别依次成等差数列,若顶点A,B,C,D处的四个数互不相同且和为1,记所有顶点上的数之和为f(n),则f(4)=( )
将正方形ABCD分割成n2(n≥2,n∈N)个全等的小正方形(图1,图2分别给出了n=2,3的情形),在每个小正方形的顶点各放置一个数,使位于正方形ABCD的四边及平行于某边的任一直线上的数都分别依次成等差数列,若顶点A,B,C,D处的四个数互不相同且和为1,记所有顶点上的数之和为f(n),则f(4)=( )| A. | 4 | B. | B6 | C. | $\frac{25}{4}$ | D. | $\frac{13}{2}$ |
9.若函数f(x)=-loga(x3+1)(a>0,a≠1)的定义域和值域都是[0,1],则a=( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 2 |
 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.